Как называется сила вызывающая изменение скорости вращения. Интерактивная модель.Движение тела на вращающемся диске
Диск вращается вокруг вертикальной оси с угловой скоростью (опыт)

 На диске, на разных расстояниях от оси вращения установлены маятники (на нитях подвешены шарики массой m).
При вращении диска маятники отклоняются от вертикали на некоторый угол а.
На диске, на разных расстояниях от оси вращения установлены маятники (на нитях подвешены шарики массой m).
При вращении диска маятники отклоняются от вертикали на некоторый угол а.
ИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЕТА (анализ данных )__
В системе отсчета, связанной, например, с помещением, шарик равномерно вращается по окружности радиусом R (расстояние от центра вращающегося шарика до оси вращения). Следовательно, на него действует сила, равная F = m ω 2 R и направленная перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести и силы натяжения нити . Для установившегося движения шарика , откуда
tg = ω 2 R/g ( тем больше, чем больше R и ω).
НЕИНЕРЦИАЛЬНАЯ СИСТЕМА ОТСЧЕТА (анализ данных )__
В системе отсчета, связанной с вращающимся диском, шарик покоится, что возможно, если сила уравновешивается равной и противоположно направленной ей силой , которая является не чем иным, как силой инерции, так как на шарик никакие другие силы не действуют. Сила F ц, называемая центробежной силой инерции , направлена по горизонтали от оси вращения диска, F ц = -m·ω 2 R.
Действию центробежных сил инерции подвергаются, например, пассажиры в движущемся транспорте на поворотах, летчики при выполнении фигур высшего пилотажа. При проектировании быстро вращающихся деталей машин (роторов, винтов самолетов и т. д.) принимаются специальные меры для уравновешивания центробежных сил инерции.
♦ Центробежная сила инерции (F ц = -m·ω 2 R)не зависит от скорости тел относительно вращающихся систем отсчета, т. е. действует на все тела, удаленные от оси вращения на конечное расстояние, независимо от того, покоятся ли они в этой системе или движутся относительно нее с какой-то скоростью.
6.3. СИЛЫ ИНЕРЦИИ, ДЕЙСТВУЮЩИЕ НА ТЕЛО, ДВИЖУЩЕЕСЯ ВО ВРАЩАЮЩЕЙСЯ СИСТЕМЕ ОТСЧЕТА _
 Диск покоится (опыт)
Диск покоится (опыт)
Шарик массой т, направленный вдоль радиуса диска со скоростью V" = const, движется по радиальной прямой ОА.
Диск вращается равномерно (со = const) (опыт)
Шарик массой т, движущийся со скоростью V" = const (V" ┴ ω), катится по кривой АВ, причем его скорость V" относительно диска изменяет свое направление. Это возможно лишь тогда, если на шарик действует сила, перпендикулярная скорости V".
Анализ опытных данных
Чтобы шарик катился по вращающемуся диску вдоль радиуса, используют жестко укрепленный вдоль радиуса диска стержень, на котором шарик движется без трения равномерно и прямолинейно со скоростью . При отклонении шарика стержень действует на него с некоторой силой .
Относительно диска (вращающейся системы отсчета) шарик движется равномерно и прямолинейно, что можно объяснить тем, что сила уравновешивается приложенной к шарику силой инерции ,
перпендикулярной скорости . Эта сила называется кориолисовой силой инерции. Сила Кориолиса
![]() .
.
Примеры проявления сил инерции
. Если тело движется в северном полушарии на север, то действующая на него сила Кориолиса ![]() направлена вправо по отношению к направлению движения, т. е. тело несколько отклонится на восток. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые, и т. д.
направлена вправо по отношению к направлению движения, т. е. тело несколько отклонится на восток. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые, и т. д.
При наблюдении сложных движений, например движения тела человека (ходьба, бег, прыжки и т.д.), кажется трудным или даже невозможным описать перемещение всех его точек. Однако, анализируя такие движения, можно заметить, что они состоят из более простых - поступательных и вращательных перемещений.
Механика поступательного движения известна читателю, поэтому раздел начинается с рассмотрения вращательного движения. Наиболее простым является вращение твердого тела вокруг неподвижной оси. Этот случай позволяет ознакомиться со спецификой, терминологией и законами вращательного движения.
5.1. КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ АБСОЛЮТНО ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ
Абсолютно твердым телом называют такое, расстояние между любыми двумя точками которого неизменно.
Размеры и форма абсолютно твердого тела не изменяются при его движении.
Понятие «абсолютно твердое тело» - физическая абстракция, так как любое тело способно к деформациям. Однако во многих случаях деформацией можно пренебречь.
Наиболее простой случай вращательного движения абсолютно твердого тела - вращение относительно неподвижной оси. Это такое движение, при котором точки тела движутся по окружностям, центры которых лежат на прямой, называемой осью вращения.
Известно, что в некоторых случаях для характеристики движения тела необязательно указывать движение всех его точек; так, например, при поступательном движении достаточно указать движение любой одной точки тела.
При вращательном движении вокруг оси точки тела перемещаются по разным траекториям, но за одно и то же время все точки и само тело поворачивается на одинаковый угол. Для характеристики вращения
проведем в плоскости, перпендикулярной оси, радиус-вектор к некоторой точке i (рис. 5.1). Временная зависимость угла α поворота радиуса-вектора относительно некоторого выделенного направления ОХ является уравнением вращательного движения твердого тела вокруг неподвижной оси:
Быстрота вращения тела характеризуется угловой скоростью, равной первой производной от угла поворота радиуса-вектора по времени:
Угловая скорость есть вектор, который направлен по оси вращения и связан с направлением вращения правилом правого винта (рис. 5.2). Вектор угловой скорости в отличие от векторов скорости и силы является скользящим: у него нет определенной точки приложения, и он может быть расположен в любом месте на оси вращения. Таким образом, задание вектора ω указывает положение оси вращения, направление вращения и модуль угловой скорости.

Быстрота изменения угловой скорости характеризуется угловым ускорением, равным первой производной от угловой скорости по времени:
или в векторной форме:
Из (5.4) видно, что вектор углового ускорения совпадает по направлению с элементарным, достаточно малым изменением вектора угловой скорости dω : при ускоренном вращении угловое ускорение направлено так же, как и угловая скорость, при замедленном вращении - противоположно ей.
Так как угловое перемещение всех точек абсолютно твердого тела одинаково, то, согласно (5.2) и (5.3), одновременно все точки тела имеют одинаковую угловую скорость и одинаковое угловое ускорение. Линейные характеристики - перемещение, скорость, ускорение - различны для разных точек. Укажем в скалярном виде связь, которая может быть выведена самостоятельно, между линейными и угловыми характеристиками для i-й точки, движущейся по окружности радиусом r i:

Рис. 5.3

В заключение приведем полученные путем интегрирования соответствующих выражений формулы кинематики вращательного движения твердого тела вокруг неподвижной оси:
уравнение равномерного вращательного движения [см. (5.2)]:
зависимость угловой скорости от времени в равнопеременном вращательном движении [см. (5.3)]:
уравнение равнопеременного вращательного движения [см. (5.1) и (5.6)]:
Полезно сопоставить эти формулы с аналогичными зависимостями для поступательного движения.
5.2. ОСНОВНЫЕ ПОНЯТИЯ. УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Момент силы _
Пусть к некоторой точке i твердого тела приложена сила F^, лежащая в плоскости, перпендикулярной оси вращения (рис. 5.4).
Моментом силы относительно оси вращения называют векторное произведение радиуса-вектора точки i на силу:
Раскрывая его, можно записать:
где β - угол между векторами r i и F i . Так как плечо силы h i = r i sinβ (см. рис. 5.4), то
Если сила действует под некоторым углом α к плоскости вращения (рис. 5.5), то ее можно разложить на две составляющие. Одна из них лежит в плоскости, перпендикулярной оси вращения, а другая параллельна этой этой оси и не оказывает влияния на вращение тела (в реальном случае она действует лишь на подшипники). Далее будут рассматриваться только силы, лежащие в плоскости, перпендикулярной оси вращения.

Рис. 5.4
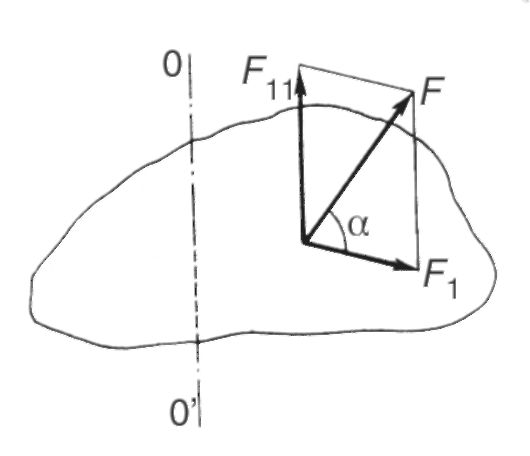
Рис. 5.5
Работа во вращательном движении
Пусть при действии силы F i (см. рис. 5.4) тело поворачивается на достаточно малый угол dα. Найдем работу этой силы.
Известное из средней школы выражение для работы силы в данном случае следует записать так:

Итак,
элементарная работа силы во вращательном движении равна произведению момента силы на элементарный угол поворота тела.
Если на тело действует несколько сил, то элементарная работа, совершенная всеми ими, определяется аналогично (5.12):
где М - суммарный момент всех внешних сил, действующих на тело.
Если при повороте тела положение радиуса-вектора изменилось от α 1 до α 2 , то работа внешних сил может быть найдена интегрированием выражения (5.13):
Момент инерции
Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от распределения ее в пространстве относительно оси. Мера инертности тела при вращении характеризуется моментом инерции тела относительно оси вращения. Укажем сначала, что
моментом инерции материальной точки относительно оси вращения называют величину, равную произведению массы точки на квадрат расстояния ее от оси:
Моментом инерции тела относительно оси называют сумму моментов инерции всех материальных точек, из которых состоит тело:


В качестве примера выведем формулу момента инерции тонкого однородного стержня длиной l и массой т относительно оси, перпендикулярной стержню и проходящей через его середину (рис. 5.6). Выберем достаточно малый участок стержня длиной dx и массой dm, удаленный от оси 00" на расстояние х. Ввиду малости этого участка он может быть принят за материальную точку, его момент инерции [см. (5.15)] равен:
Масса элементарного участка равна произведению линейной плотности т/l, умноженной на длину элементарного участка: dm = (m/l) dx Подставив это выражение в (5.18), получим
Чтобы найти момент инерции всего стержня, проинтегрируем выражение (5.19) по всему стержню, т.е. в пределах от -1/2 до +1/2:

Приведем выражения для моментов инерции разных симметричных тел массой т:
полого однородного цилиндра (обруча) с внутренним радиусом r и внешним R относительно оси ОО", совпадающей с геометрической осью цилиндра (рис. 5.7):
сплошного однородного цилиндра (r = 0) или диска [см. (5.21)]:
однородного шара относительно оси, проходящей через его центр:
прямоугольною параллелепипеда относительно оси ОО", проходящей через его центр перпендикулярно плоскости основания (рис. 5.8):
Во всех перечисленных примерах ось вращения проходит через центр масс тела. При решении задач для определения момента инерции тела относительно оси, не проходящей через центр масс, можно воспользоваться теоремой Гюйгенса. Согласно этой теореме, момент инерции тела относительно некоторой оси OO":
где J 0 - момент инерции относительно параллельной оси, проходящей через центр масс тела OO"; т - масса тела; d - расстояние между двумя параллельными осями (рис. 5.9). Единицей момента инерции является килограмм-метр в квадрате (кг-м 2).

Момент импульса
Моментом импульса (момент количества движения) материальной точки, вращающейся относительно некоторой оси, называется величина, равная произведению импульса точки на расстоянии ее до оси вращения:
Момент импульса тела, вращающегося относительно некоторой оси, равен сумме моментов импульсов точек, из которых состоит данное тело:

Так как угловая скорость всех точек твердого тела одинакова, выне-ся ω за знак суммы [см. (5.29)], получим:
(/ - момент инерции тела относительно оси), или в векторной форме:
Итак, момент импульса равен произведению момента инерции точки на угловую скорость. Отсюда следует, что направления векторов момента импульса и угловой скорости совпадают. Единицей момента импульса является килограмм-метр в квадрате в секунду (кг? м 2 ? с -1).
Формулу (5.31) полезно сравнить с аналогичной формулой для импульса в поступательном движении.
Кинетическая энергия вращающегося тела
При вращении тела его кинетическая энергия складывается из кинетических энергий отдельных точек тела. Для твердого тела:
Полезно сопоставить выражение (5.32) с аналогичным выражением для поступательного движения.
Продифференцировав (5.32), получим элементарное изменение кинетической энергии во вращательном движении:
Основное уравнение динамики вращательного движения
Пусть твердое тело, на которое действовали внешние силы, повернулось на достаточно малый угол da. Приравняем элементарную работу всех внешних сил при таком повороте [см. (5.13)] элементарному изменению кинетической энергии [см. (5.33)]: M dα = J ω dω , откуда:

Это и есть основное уравнение динамики вращательного движения. Из (5.35) видно, что момент инерции характеризует инерционные свойства тела во вращательном движении: при действии внешних сил угловое ускорение тела тем больше, чем меньше момент инерции тела.
Основное уравнение для вращательного движения играет ту же роль, что и второй закон Ньютона для поступательного. Физические величины, входящие в это уравнение, аналогичны соответственно силе, массе и ускорению.
Из (5.34) следует, что:
Производная от момента импульса тела по времени равна равнодействующему моменту всех внешних сил.
Зависимость углового ускорения от момента силы и момента инерции можно продемонстрировать с по-

мощью прибора, изображенного на рис. 5.10. Под действием груза 1, подвешенного на нити, перекинутой через блок, крестовина ускоренно вращается. Перемещая грузики 2 на разные расстояния от оси вращения, можно изменять момент инерции крестовины. Меняя грузы, т.е. моменты сил, и момент инерции, можно убедиться, что угловое ускорение возрастает при увеличении момента силы или уменьшении момента инерции.
5.3. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
Рассмотрим частный случай вращательного движения, когда суммарный момент внешних сил равен нулю. Как видно из (5.37), dL/dt = 0 при М = 0, откуда
Это положение известно под названием закона сохранения момента импульса: если суммарный момент всех внешних сил, действующих на тело, равен нулю, то момент импульса этою тела остается постоянным.
Опуская доказательство, отметим, что закон сохранения момента импульса справедлив не только для абсолютно твердого тела.
Наиболее интересные применения этого закона связаны с вращением системы тел вокруг общей оси. При этом необходимо учитывать векторный характер момента импульса и угловых скоростей. Так, для системы, состоящей из N тел, вращающихся вокруг общей оси, закон сохранения момента импульса можно записать в форме:
Рассмотрим некоторые примеры, иллюстрирующие этот закон.
Гимнаст, выполняющий сальто (рис. 5.11), в начальной фазе сгибает колени и прижимает их к груди, уменьшая тем самым момент инерции и увеличивая угловую скорость вращения вокруг горизонтальной оси, проходящей через центр масс. В конце прыжка тело выпрямляется, момент инерции возрастает, угловая скорость уменьшается. Фигурист, совершающий вращение вокруг вертикальной оси (рис. 5.12), в начале вращения приближает руки к корпусу, тем самым уменьшая момент инерции и увеличивая угловую скорость. В конце вращения происходит обратный процесс: при разведении рук увеличивается момент инерции и уменьшается угловая скорость, что позволяет легко остановиться.

Такое же явление может быть продемонстрировано на скамье Жуковского, которая представляет собой легкую горизонтальную платформу, вращающуюся с малым трением вокруг вертикальной оси. При изменении положения рук изменяются момент инерции и угловая скорость (рис. 5.13), момент импульса остается постоянным. Для усиления демонстрационного эффекта в руках человека гантели. На скамье Жуковского можно продемонстрировать векторный характер закона сохранения момента импульса.
Экспериментатор, стоящий на неподвижной скамье, получает от помощника велосипедное колесо, вращающееся вокруг вертикальной оси (рис. 5.14, слева). В этом случае момент импульса системы человек и платформа-колесо определяется только моментом импульса колеса:
здесь J ч - момент инерции человека и платформы; J K и ω κ - момент инерции и угловая скорость колеса. Так как момент внешних сил относительно вертикальной оси равен нулю, то L сохраняется (L = const).
Если экспериментатор повернет ось вращения колеса на 180° (рис. 5.14, справа), то момент импульса колеса будет направлен противоположно первоначальному и равен J K ω K . Так как вектор момента импульса колеса изменяется, а момент импульса системы сохраняется, то неизбежно должен измениться и момент импульса, человека и платформы, он уже не будет равен нулю 1 . Момент импульса системы в этом случае
1 Небольшим несовпадением оси колеса с осью вращения платформы можно пренебречь.



По формуле (5.42) можно приближенно оценить момент инерции тела человека вместе с платформой, для чего необходимо измерить ω κ , ω 4 и найти J k . Способ измерения угловых скоростей равномерного вращения известен читателю. Зная массу колеса и предполагая, что в основном масса распределена по ободу, по формуле (5.22) можно определить J k . Для уменьшения ошибки можно утяжелить обод велосипедного колеса, проложив по нему специальные шины. Человек должен располагаться симметрично оси вращения.
Более простой вариант рассмотренной демонстрации состоит в том, что человек, стоящий на скамье Жуковского, сам приводит во вращение колесо, которое он держит на вертикальной оси. При этом человек и платформа начинают вращаться в противоположные стороны (рис. 5.15).
5.4. ПОНЯТИЕ О СВОБОДНЫХ ОСЯХ ВРАЩЕНИЯ
Тело, вращающееся вокруг фиксированной оси, в общем случае действует на подшипники или другие устройства, которые сохраняют неизменным положение этой оси. При больших угловых скоростях и моментах инерции эти воздействия могут быть значительными. Однако в любом теле можно выбрать такие оси, направление которых при вращении будет сохраняться без каких-либо специальных устройств. Чтобы понять, какому условию должен удовлетворять выбор таких осей, рассмотрим следующий пример.

Сопоставляя (5.43) с координатами центра масс, замечаем, что силы, действующие на ось, уравновешиваются, если ось вращения проходит через центр масс.
Таким образом, если ось вращения проходит перпендикулярно стержню через центр масс, то воздействия на эту ось со стороны вращающегося тела не будет. Если при этом убрать подшипники, то ось вращения начнет перемещаться, сохраняя неизменным положение в пространстве, а тело будет продолжать вращение вокруг этой оси.
Оси вращения, которые без специального закрепления сохраняют свое направление в пространстве, называют свободными. Примерами таких осей являются оси вращения Земли и волчка, ось всякого брошенного и свободно вращающегося тела и т.п.
У тела произвольной формы всегда имеется по крайней мере три взаимно перпендикулярные оси, проходящие через центр масс, которые могут быть свободными осями вращения. Эти оси называют главными осями инерции. Хотя все три главные оси инерции являются свободными, наиболее устойчивым будет вращение вокруг оси с наибольшим моментом инерции. Дело в том, что в результате неизбежного действия внешних сил, например трения, а также в связи с тем, что трудно задать вращение точно вокруг определенной оси, вращение вокруг остальных свободных осей неустойчиво.
В некоторых случаях, когда тело вращается около свободной оси с малым моментом инерции, оно само изменяет эту ось на ось с наибольшим моментом.
Это явление демонстрируют следующим опытом. К электродвигателю подвешена на нити цилиндрическая палочка, которая может вращаться вокруг своей геометрической оси (рис. 5.17, а). Момент инерции относительно этой оси J 1 = тR 2 /2. При достаточно большой угловой скорости палочка изменит свое положение (рис. 5.17, б). Момент инерции относительно новой оси равен J 2 = ml 2 /12. Если l 2 >6R 2 , то и J 2 > J 1 . Вращение вокруг новой оси будет устойчивым.
Читатель может самостоятельно на опыте убедиться, что вращение брошенной спичечной коробки устойчиво относительно оси, проходящей перпендикулярно большей грани, и неустойчиво или менее устойчиво относительно осей, проходящих перпендикулярно другим граням (см. рис. 5.8).
Вращение животных и человека в свободном полете и при различных прыжках происходит вокруг свободных осей с наибольшим или наименьшим моментом инерции. Так как положение центра масс зависит от позы тела, то при разных позах будут и различные свободные оси.

5.5. ПОНЯТИЕ О СТЕПЕНЯХ СВОБОДЫ
Положение свободной материальной точки в пространстве задается тремя независимыми координатами: х, у, z. Если точка не свободна, а перемещается, например, по некоторой поверхности, то не все три координаты будут независимыми.

Независимые переменные, характеризующие положение механической системы, называют степенями свободы.
У свободной материальной точки три степени свободы, в рассмотренном примере - две степени свободы. Так как молекулу одноатомного газа можно рассматривать как материальную точку, следовательно, такая свободная молекула тоже имеет три степени свободы.
Еще некоторые примеры.
Две материальные точки 1 и 2 жестко связаны друг с другом. Положение обеих точек задано шестью координатами x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , на которые наложены одно ограничение и одна связь, математически выражаемая в форме уравнения:
Физически это означает, что расстояние между материальными точками всегда l. В этом случае число степеней свободы равно 5. Рассмотренный пример является моделью двухатомной молекулы.
Три материальные точки 1, 2 и 3 жестко связаны друг с. другом. Девять координат характеризуют положение такой системы: x 1 , y 1 , z 1 , x 2 , y 2 , z 2 , x 3 , y 3 , z 3 . Однако три связи между точками обусловливают независимость только шести координат. Система имеет шесть степеней свободы. Так как положение трех точек, не лежащих на одной прямой, однозначно определяет положение твердого тела, то и твердое тело имеет шесть степеней свободы.
Такое же число степеней свободы (шесть) имеют трехатомные и многоатомные молекулы, если эти молекулы рассматривать как жесткие образования.
1 Если для зависимой координаты из (5.44) получают мнимую величину, это означает, что выбранные независимые координаты не соответствуют каким-либо точкам, расположенным на сфере заданного радиуса.
В реальных многоатомных молекулах атомы находятся в колебательных движениях, поэтому число степеней свободы таких молекул более шести.
Число степеней свободы определяет не только число независимых переменных, характеризующих положение механической системы, но и, что очень важно, число независимых перемещений системы. Так, три степени свободы свободной материальной точки означают, что любое перемещение точки можно разложить на независимые перемещения по трем осям координат. Так как точка не имеет размеров, то говорить о ее вращении не имеет смысла. Итак, материальная точка имеет три степени свободы поступательного движения. Материальная точка на плоскости, сфере или иной поверхности имеет две степени свободы поступательного движения. Перемещение материальной точки вдоль кривой (условный пример - движение поезда по рельсам) соответствует одной степени свободы поступательного движения.
Твердое тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы вращательного движения. Колесо поезда имеет две степени свободы: одна - вращательного движения, а другая - поступательного (перемещение оси колеса вдоль рельса). Шесть степеней свободы твердого тела означают, что любое перемещение этого тела можно разложить на составляющие: перемещение центра масс раскладывается на три поступательных движения по осям координат, а вращение состоит из трех более простых поворотов относительно осей координат, проходящих через центр масс.
На рис. 5.18-5.20 показаны шарнирные соединения, соответствующие одной, двум и трем степеням свободы.

Рис. 5.18

Рис. 5.19

Рис. 5.20
5.6. ЦЕНТРИФУГИРОВАНИЕ
Центрифугированием называется процесс разделения (сепарации) неоднородных систем, например частиц от жидкостей, в которых они находятся, обусловленный их вращением.
Рассмотрим разделение неоднородных систем в поле силы тяжести. Предположим, что имеется водная суспензия частиц различной плотности. Со временем благодаря действию силы тяжести и выталкивающей силы F A происходит расслаивание частиц: частицы с большей, чем у воды, плотностью тонут, частицы с меньшей, чем у воды, плотностью всплывают. Результирующая сила, действующая, например, на более плотную отдельную частицу, равна:
где ρ 1 - плотность вещества частицы; ρ - плотность воды; V - объем частицы.
Если значения ρ 1 и ρ мало отличаются друг от друга, то сила F p мала и расслоение (осаждение) происходит достаточно медленно. В центрифуге (сепараторе) такое разделение производят принудительно, вращая разделяемую среду.
Рассмотрим физику этого явления.
Пусть рабочий объем центрифуги (рис. 5.21: а - внешний вид; б - схема рабочего объема) полностью занят какой-либо однородной жидкостью. Выделим мысленно небольшой объем V этой жидкости, находящийся на расстоянии r от оси вращения OO". При равномерном вращении центрифуги на выделенный объем кроме силы тяжести и выталкивающей силы, которые уравновешивают друг друга, действует центростремительная сила. Это сила со стороны окружающей объем жидкости. Она, естественно, направлена к оси вращения и равна:
где ρ - плотность жидкости.
Предположим теперь, что выделенный объем V - это сепарируемая частица, плотность вещества которой ρ 1 (ρ 1 Φ ρ). Сила, действующая на частицу со стороны окружающей жидкости, не изменится, как это видно из формулы (5.45).
Для того чтобы частица вращалась вместе с жидкостью, на нее должна действовать центростремительная сила, равная:
где m 1 - масса частицы, а ρ 1 - соответствующая ей плотность.

Рис. 5.21
Если F > F 1 , то частица перемещается к оси вращения. Если F < F 1 , то воздействия на частицу со стороны жидкости будет недостаточно, чтобы удержать ее на круговой траектории, и частица по инерции начнет перемещаться к периферии. Эффект сепарации определяется превышением силы F, действующей со стороны жидкости на выделенную частицу, над тем значением центростремительной силы F 1 , которое обусловливает движение по окружности:
Это выражение показывает, что эффект центрифугирования тем больше, чем больше различие плотностей сепарируемых частиц и жидкости, а также существенно зависит от угловой скорости вращения 1 .
Сравним разделение центрифугированием с разделением с помощью силы тяжести:

1 Сила тяжести и выталкивающая сила при выводе формулы (5.47) не учитываются, так как они направлены вдоль оси вращения и не оказывают принципиального влияния на центрифугирование.
Ультрацентрифуги способны разделить частицы размером менее 100 нм, взвешенные или растворенные в жидкости. Они нашли широкое применение в медико-биологических исследованиях для разделения биополимеров, вирусов и субклеточных частиц.
Быстрота сепарации особенно важна в биологических и биофизических исследованиях, так как со временем может существенно измениться состояние изучаемых объектов.
15.2.1 При вращении твердого тела вокруг неподвижной оси силы давления на опоры (подшипники, подпятник) переменны по величине, носят циклический характер и могут значительно превышать силы давления, которые испытывают опоры при отсутствии вращения. При вращении тела не исключена также опасность резонанса.
Например, пусть центр тяжести вала массой 10кг, вращающегося с постоянной частотой 10 000об/мин, смещен от его оси на расстояние e =1мм. Действующая на него центробежная (нормальная) сила инерции равна
Что более чем в 200 раз превышает давление в опорах от веса вала.
При ускоренном или замедленном вращения вала на опоры действуют также циклические давления от касательных составляющих сил инерции, которые также могут достигать значительных величин и стать причиной резонанса и разрушения опор.
15.2.2Для определения реакций в опорах вращающегося тела воспользуемся принципом Даламбера.
Пусть к телу массы М
приложены активные силы . Освободим тело от связей, заменив их реакциями ![]() и . Добавим к этим силам главный вектор сил инерции и главный момент сил инерции . Тело находится в равновесии под действием произвольной пространственной системы сил. Составим шесть уравнений равновесия:
и . Добавим к этим силам главный вектор сил инерции и главный момент сил инерции . Тело находится в равновесии под действием произвольной пространственной системы сил. Составим шесть уравнений равновесия:
![]() ;
;
![]() ;
;
![]() .
.
Используя теорему о движении центра масс и раскладывая силы инерции, действующие на точки, на нормальные и касательные составляющие можно преобразовать эту систему уравнений равновесия [?] в следующую:
![]() .
.
Если тело не вращается вокруг оси Z, , то получим уравнения статики:
![]() ;
;
![]() ;
;
![]() ;
;
из которых можно определить статические реакции опор .
Статическим реакциями называются части полных реакций, которые статически уравновешивают приложенные внешние силы . Уравнения для их определения получают, положив в выражениях для полных реакций .
Динамическими реакциями называют части полных реакций, которые уравновешивают силы инерции точек тела вращения. Уравнения для их определения получают, вычтя из выражений для полных реакций статические реакции. Динамические реакции зависят от ε и ω.
Статически уравновешенным
называют тело, имеющее ось вращения, если центр масс этого тела лежит на оси вращения. В этом случае главный вектор сил инерции равен нулю, то есть ![]() , а главный момент сил инерции не равен нулю, то есть . Динамические реакции образуют в опорах циклически изменяющуюся пару сил. Опоры испытывают вибрации, которые могут привести к их усталости и разрушению, особенно в тех случаях, когда циклическая частота мест крепления близка к угловой скорости вращения тела.
, а главный момент сил инерции не равен нулю, то есть . Динамические реакции образуют в опорах циклически изменяющуюся пару сил. Опоры испытывают вибрации, которые могут привести к их усталости и разрушению, особенно в тех случаях, когда циклическая частота мест крепления близка к угловой скорости вращения тела.
Основные понятия.
Момент силы относительно оси вращения – это векторное призведение радиус-вектора на силу.
Момент силы – это вектор, направление которого определяется по правилу буравчика (правого винта) в зависимости от направления силы, действующей на тело. Момент силы направлен вдоль оси вращения и не имеет конкретной точки приложения.
Численное значение данного вектора определяется по формуле:
M=r×F × sina (1.15),
где a- угол между радиус-вектором и направлением действия силы.
Если a=0 или p , момент силы М=0 , т.е. сила, проходящяя через ось вращения или совпадающяя с ней, вращения не вызывает.
Наибольший по модулю вращающий момент создается, если сила действует под углом a=p/2 (М > 0) или a=3p/2 (М < 0).
Используя понятие плеча силы (плечо силы d – это перпендикуляр, опущенный из центра вращения на линию действия силы), формула момента силы принимает вид:
Где ![]() (1.16)
(1.16)
Правило моментов сил (условие равновесия тела, имеющего неподвижную ось вращения):
Для того, чтобы тело, имеющее неподвижную ось вращения, находилось в равновесии, необходимо, чтобы алгебраическая сумма моментов сил, действующих на данное тело, равнялась нулю.
S М i =0 (1.17)
Единицей измерения момента силы в системе СИ является [Н×м]
При вращательном движении инертность тела зависит не только от его массы, но и от распределения ее в пространстве относительно оси вращения.
Инертность при вращении характеризуется моментом инерциитела относительно оси вращения J.
Момент инерции материальной точки относительно оси вращения – это величина, равная произведению массы точки на квадрат ее расстояния от оси вращения:
J i =m i × r i 2 (1.18)
Моментом инерции тела относительно оси называется сумма моментов инерции материальных точек, из которых состоит тело:
J=S m i × r i 2 (1.19)
Момент инерции тела зависит от его массы и формы, а также от выбора оси вращения. Для определения момента инерции тела относительно некоторой оси используется теорема Штейнера-Гюйгенса:
J=J 0 +m× d 2 (1.20),
где J 0 – момент инерции относительно параллельной оси, проходящей через цент масс тела, d – расстояние между двумя параллельными осями. Момент инерции в СИ измеряется в [кг×м 2 ]
Момент инерции при вращательном движении туловища человека определяют опытным путем и рассчитывают приблизительно по формулам для цилиндра, круглого стержня или шара.
Момент инерции человека относительно вертикальной оси вращения, которая проходит через центр масс (центр масс тела человека находится в сагиттальной плоскости немного впереди второго крестцового позвонка), в зависимости от положения человека, имеет следующие значения: при стойке “смирно” – 1,2 кг×м 2 ; при позе «арабеск» – 8 кг×м 2 ; в горизонтальном положении – 17 кг× м 2 .
Работа во вращательном движении совершается при вращении тела под действием внешних сил.
Элементарная работа силы во вращательном движении равна произведению момента силы на элементарный угол поворота тела:
dA i =M i × dj (1.21)
Если на тело действует несколько сил, то элементарная работа равнодействующей всех приложенных сил определяется по формуле:
dA=M× dj (1.22),
где М – суммарный момент всех внешних сил, действующих на тело.
Кинетическая энергия вращающегося тела W к зависит от момента инерции тела и угловой скорости его вращения:
Момент импульса (момент количества движения) – величина, численно равная произведению импульса тела на радиус вращения.
L=p× r=m× V× r (1.24).
После соответствующих преобразований можно записать формулу для определения момента импульса в виде:
(1.25).
Момент импульса – вектор, направление которого определяется по правилу правого винта. Единицей измерения момента импульса в СИ является [кг×м 2 /с]
Основные законы динамики вращательного движения.
Основное уравнение динамики вращательного движения:
Угловое ускорение тела, совершающего вращательное движение, прямо пропорционально суммарному моменту всех внешних сил и обратно пропорционально моменту инерции тела.
(1.26).
Данное уравнение играет ту же роль при описании вращательного движения, что и второй закон Ньютона для поступательного движения. Из уравнения видно, что при действии внешних сил угловое ускорение тем больше, чем меньше момент инерции тела.
Второй закон Ньютона для динамики вращательного движения можно записать в ином виде:
(1.27),
т.е. первая производная от момента импульса тела по времени равна суммарному моменту всех внешних сил, действующих на данное тело.
Закон сохранения момента импульса тела:
Если суммарный момент всех внешних сил, действующих на тело, равен нулю, т.е.
S M i =0 , тогда dL/dt=0 (1.28).
Из этого следует или (1.29).
Это утверждение составляет сущность закона сохранения момента импульса тела, который формулируется следующим образом:
Момент импульса тела остается постоянным, если суммарный момент внешних сил, действующих на вращающееся тело, равен нулю.
Этот закон является справедливым не только для абсолютно твердого тела. Примером является фигурист, который выполняет вращение вокруг вертикальной оси. Прижимая руки, фигурист уменьшает момент инерции и увеличивает угловую скорость. Чтобы затормозить вращения, он, наоборот, широко разводит руки; в результате момент инерции увеличивается, и угловая скорость вращения уменьшается.
В заключение приведем сравнительную таблицу основных величин и законов, характеризующих динамику поступательного и вращательного движений.
Таблица 1.4.
| Поступательное движение | Вращательное движение | ||
| Физическая величина | Формула | Физическая величина | Формула |
| Масса | m | Момент инерции | J=m×r 2 |
| Сила | F | Момент силы | M=F×r, если |
| Импульс тела (количество движения) | p=m×V | Момент импульса тела | L=m×V×r; L=J×w |
| Кинетическая энергия | Кинетическая энергия | ||
| Механическая работа | dA=FdS | Механическая работа | dA=Mdj |
| Основное уравнение динамики поступательного движения | Основное уравнение динамики вращательного движения | , | |
| Закон сохранения импульса тела |
или
| Закон сохранения момента импульса тела | или SJ i w i =const, если |
Центрифугирование.
Разделение неоднородных систем, состоящих из частиц различной плотности, может быть произведено под действием силы тяжести и силы Архимеда (выталкивающей силы). Если есть водная суспензия частиц различной плотности, то на них действует результирующая сила
F р =F т – F А =r 1 ×V×g - r×V×g , т.е
F р =(r 1 - r)× V×g (1.30)
где V – объем частицы, r 1 и r – соответственно плотности вещества частицы и воды. Если плотности незначительно отличаются друг от друга, то результирующая сила мала и расслоение (осаждение) происходит достаточно медленно. Поэтому используют принудительное разделение частиц за счет вращения разделяемой среды.
Центрифугированием называется процесс разделения (сепарации) неоднородных систем, смесей или взвесей, состоящих из частиц различной массы, происходящий под действием центробежной силы инерции.
Основу центрифуги составляет ротор с гнездами для пробирок, расположенный в закрытом корпусе, который приводится во вращение электродвигателем. При вращении с достаточно высокой скоростью ротора центрифуги частицы взвеси, различные по масссе, под действием центробежной силы инерции распределяются слоями на различной глубине, а наиболее тяжелые осаждаются на дне пробирки.
Можно показать, что сила, под действием которой происходит сепарация, определяется по формуле:
![]() (1.31)
(1.31)
где w - угловая скорость вращения центрифуги, r – расстояние от оси вращения. Эффект центрифугирования тем больше, чем больше различие плотностей сепарируемых частиц и жидкости, а также существенно зависит от угловой скорости вращения.
Ультрацентрифуги, работающие при скорости вращения ротора порядка 10 5 –10 6 оборотов в минуту, способны разделить частицы размером менее 100нм, взвешенные или растворенные в жидкости. Они нашли широкое применение в медико-биологических исследованиях.
С помощью ультрацентрифугирования можно разделить клетки на органеллы и макромолекулы. Вначале оседают (седиментируют) более крупные части (ядра, цитоскелет). При дальнейшем увеличении скорости центрифугирования последовательно оседают более мелкие частицы – сначала митохондрии, лизосомы, затем микросомы и, наконец, рибосомы и крупные макромолекулы. При центрифугировании различные фракции оседают с различной скоростью, образуя в пробирке отдельные полосы, которые можно выделить и исследовать. Фракционированные клеточные экстракты (бесклеточные системы) широко используют для изучения внутриклеточных процессов, например для изучения биосинтеза белка, расшифровки генетического кода.
Для стерилизации наконечников в стоматологии используется масляный стерилизатор с центрифугой, с помощью которой удаляется излишнее масло.
Центрифугирование можно использовать для осаждения частиц, взвешенных в моче; отделения форменных элементов от плазмы крови; разделения биополимеров, вирусов и субклеточных структур; контроля за чистотой препарата.
Задания для самоконтроля знаний.
Задание1 . Вопросы для самоконтроля.
Чем отличается равномерное движение по окружности от равномерного прямолинейного движения? При каком условии тело будет двигаться равномерно по окружности?
Объясните причину того, что равномерное движение по окружности происходит с ускорением.
Может ли криволинейное движение происходить без ускорения?
При каком условии момент силы равен нулю? принимает наибольшее значение?
Укажите границы применимости закона сохранения импульса, момента импульса.
Укажите особенности сепарации под действием силы тяжести.
Почему разделение белков с различными молекулярными массами можно проводить при помощи центрифугирования, а метод фракционной перегонки оказывается неприемлемым?
Задание 2 . Тесты для самоконтроля.
Вставьте пропущенное слово:
Изменение знака угловой скорости свидетельствует об изменении_ _ _ _ _ вращательного движения.
Изменение знака углового ускорения свидетельствует об изменении_ _ _ вращательного движения
Угловая скорость равна _ _ _ _ _производной угла поворота радиус-вектора по времени.
Угловое ускорение равно _ _ _ _ _ _производной угла поворота радиус-вектора по времени.
Момент силы равен_ _ _ _ _, если направление действующей на тело силы совпадает с осью вращения.
Найдите правильный ответ:
Момент силы зависит только от точки приложения силы.
Момент инерции тела зависит только от массы тела.
Равномерное движение по окружности происходит без ускорения.
А. Правильно. В. Неправильно.
Скалярними являются все перечисленные величины, за исключением
А. момента силы;
В. механической работы;
С. потенциальной энергии;
Д. момента инерции.
Векторными величинами являются
А. угловая скорость;
В. угловое ускорение;
С. момент силы;
Д. момент импульса.
Ответы : 1 – направления; 2 – характера; 3 – первой; 4 – второй; 5 – нулю; 6 – В; 7 – В; 8 – В; 9 – А; 10 – А, В, С, Д.
Задание 3 . Получите связь между единицами измерения:
линейной скорости см/мин и м/с;
углового ускорения рад/мин 2 и рад/с 2 ;
момента силы кН×см и Н×м;
импульса тела г×см/с и кг×м/с;
момента инерции г×см 2 и кг×м 2 .
Задание 4 . Задачи медико-биологического содержания.
Задача №1. Почему в полетной фазе прыжка спортсмен не может никакими движениями изменить траекторию движения центра тяжести тела? Совершают ли мышцы спортсмена работу при изменении положения частей тела в пространстве?
Ответ: Движениями в свободном полете по параболе спортсмен может только изменять расположение тела и его отдельных частей относительно своего центра тяжести, который в данном случае является центром вращения. Спортсмен совершает работу по изменению кинетической энергии вращения тела.
Задача №2. Какую среднюю мощность развивает человек при ходьбе, если продолжительность шага 0,5с? Считать, что работа затрачивается на ускорение и замедление нижних конечностей. Угловое перемещение ног около Dj=30 о. Момент инерции нижней конечности равен 1,7кг× м 2 . Движение ног рассматривать как равнопеременное вращательное.
Решение:
1)Запишем краткое условие задачи: Dt= 0,5с; Dj =30 0 =p/ 6; I =1,7кг× м 2
2) Определим работу за один шаг (правая и левая нога): A= 2×Iw 2 / 2=Iw 2 .
Используя формулу средней угловой скорости w ср =Dj/Dt, получим: w= 2w ср = 2×Dj/Dt; N=A/Dt= 4×I×(Dj) 2 /(Dt) 3
3) Подставим числовые значения: N =4× 1,7× (3,14) 2 /(0,5 3 × 36)=14,9(Вт)
Ответ: 14,9 Вт.
Задача №3. Какова роль движения рук при ходьбе?
Ответ : Движение ног, перемещающихся в двух параллельных плоскостях, находящихся на некотором расстоянии друг от друга, создает момент сил, стремящийся повернуть корпус человека вокруг вертикальной оси. Руками человек размахивает «навстречу» движению ног, создавая тем самым момент сил противоположного знака.
Задача №4. Одним из направлений усовершенствования бормашин, применяемых в стоматологии, является увеличение скорости вращения бора. Скорость вращения борного наконечника в ножных бормашинах составляет 1500 оборотов в минуту, в стационарных электробормашинах – 4000 об/мин, в турбинных бормашинах – уже достигает 300000 об/мин. Зачем разрабатываются новые модификации бормашин с большим числом оборотов в единицу времени?
Ответ: Дентин в несколько тысяч раз более восприимчив к болевым ощущениям, чем кожа: на 1мм 2 кожи приходится 1-2 болевые точки, а на 1мм 2 дентина резцов – до 30000 болевых точек. Увеличение числа оборотов по данным физиологов уменьшает боль при обработке кариозной полости.
Задание 5 . Заполните таблицы:
Таблица №1 . Проведите аналогию между линейными и угловыми характеристиками вращательного движения и укажите связь между ними.
Таблица №2.
Задание 6. Заполните ориентировочную карту действия:
| Основные задания | Указания | Ответы |
| Для чего в начальной стадии исполнения сальто гимнаст сгинает колени и прижимает их к груди, а в конце вращения выпрямляет тело? | Используйте для анализа процесса понятие момента импульса и закон сохранения момента импульса. | |
| Объясните, почему стоять на цыпочках (или держать тяжелый груз) так тяжело? | Рассмотрите условия равновесия сил и их моментов. | |
| Как изменится угловое ускорение при увеличении момента инерции тела? | Проанализируйте основное уравнение динамики вращательного движения. | |
| Как зависит эффект центрифугирования от разности в плотностях жидкости и частиц, которые сепарируются? | Рассмотрите силы, действующие при центрифугировании и соотношения между ними |
Глава 2. Основы биомеханики.
Вопросы.
Рычаги и сочленения в опорно-двигательном аппарате человека. Понятие о степенях свободы.
Виды сокращения мышц. Основные физические величины, описывающие мышечные сокращения.
Принципы двигательной регуляции у человека.
Методы и приборы для измерения биомеханических характеристик.
2.1. Рычаги и сочленения в опорно-двигательном аппарате человека.
Анатомия и физиология двигательного аппарата человека обладают следующими особенностями, которые необходимо учитывать при биомеханических расчетах: движения тела определяются не только мышечными силами, но и внешними силами реакции, силой тяжести, инерционными силами, а также упругими силами и трением; структура двигательного аппарата допускает исключительно вращательные движения. С помощью анализа кинематических цепей поступательные движения могут быть сведены к вращательным движениям в суставах; движения управляются с помощью очень сложного кибернетического механизма, так что происходит постоянное изменение ускорений.
Опорно-двигательный аппарат человека состоит из сочлененных между собой костей скелета, к которым в определенных точках прикрепляются мышцы. Кости скелета действуют как рычаги, которые имеют точку опоры в сочленениях и приводятся в движение силой тяги, возникающей при сокращении мышц. Различают три вида рычага :
1) Рычаг, к которому действующая сила F и сила сопротивления R приложены по разные стороны от точки опоры. Примером такого рычага является череп, рассматриваемый в сагиттальной плоскости.
2) Рычаг, у которого действующая сила F и сила сопротивления R приложены по одну сторону от точки опоры, причем, сила F приложена к концу рычага, а сила R - ближе к точке опоры. Данный рычаг дает выигрыш в силе и проигрыш в расстоянии, т.е. является рычагом силы . Пример - действие свода стопы при подъеме на полупальцы, рычаги челюстно-лицевого отдела (рис. 2.1). Движения жевательного аппарата очень сложны. При закрывании рта поднимание нижней челюсти из положения максимального опускания до положения полного смыкания ее зубов с зубами верхней челюсти осуществляется движением мышц, поднимающих нижнюю челюсть. Эти мышцы действуют на нижнюю челюсть как на рычаг второго рода с точкой опоры в суставе (дающий выигрыш при жевании в силе).
3) Рычаг, у которого действующая сила приложена ближе к точке опоры, чем сила сопротивления. Данный рычаг является рычагом скорости , т.к. дает проигрыш в силе, но выигрыш в перемещении. Пример - кости предплечья.


Рис. 2.1. Рычаги челюстно-лицевого отдела и свода стопы.
Большинство костей скелета находится под действием нескольких мышц, развивающих усилия по различным направлениям. Равнодействующая их находится путем геометрического сложения по правилу параллелограмма.
Кости опорно-двигательного аппарата соединяются между собой в сочленениях или суставах. Концы костей, образующих сустав, удерживаются вместе с помощью плотно охватывающей их суставной сумки, а также прикрепленных к костям связок. Для уменьшения трения соприкасающиеся поверхности костей покрыты гладким хрящом и между ними имеется тонкий слой клейкой жидкости.
Первой ступенью биомеханического анализа двигательных процессов является определение их кинематики. На основе такого анализа строятся абстрактные кинематические цепи, подвижность или устойчивость которых может быть проверена исходя из геометрических соображений. Различают замкнутые и разомкнутые кинематические цепи, образуемые суставами и расположенными между ними жесткими звеньями.
Состояние свободной материальной точки в трехмерном пространстве задается тремя независимыми координатами – х, y, z . Независимые переменные, которые характеризуют состояние механической системы, называются степенями свободы . У более сложных систем количество степеней свободы может быть выше. Вообще, количество степеней свободы определяет не только количество независимых переменных (что характеризует состояние механической системы), но и количество независимых перемещений системы.
Число степеней свободы является основной механической характеристикой сустава, т.е. определяет число осей , вокруг которых возможно взаимное вращение сочленненых костей. Обусловлено оно главным образом геометрической формой поверхности костей, соприкасающихся в суставе.
Максимальное число степеней свободы в суставах – 3.
Примерами одноосного (плоского) сочленения в организме человека являются плечелоктевое, надпяточное и фаланговые соединения. Они допускают только возможность сгибания и разгибания с одной степенью свободы. Так, локтевая кость с помощью полукруглой выемки охватывает цилиндрический выступ на плечевой кости, который и служит осью сустава. Движения в суставе – сгибание и разгибание в плоскости, перпендикулярной оси сустава.
Лучезапястный сустав, в котором осуществляется сгибание и разгибание, а также приведение и отведение, можно отнести к суставам с двумя степенями свободы.
К суставам с тремя степенями свободы (пространственное сочленение) относятся тазобедренное и лопаточно-плечевое сочленение. Например, в лопаточно-плечевом сочленении шаровидная головка плечевой кости входит в сферическую впадину выступа лопатки. Движения в суставе – сгибание и разгибание (в сагиттальной плоскости), приведение и отведение (в фронтальной плоскости) и вращение конечности вокруг продольной оси.
Замкнутые плоские кинематические цепи обладают числом степеней свободы f F , которое вычисляется по числу звеньев n следующим образом:
Ситуация для кинематических цепей в пространстве более сложная. Здесь выполняется соотношение
![]() (2.2)
(2.2)
гдеf i - число ограничений степеней свободы i- го звена.
В любом теле можно выбрать такие оси, направление которых при вращении будет сохраняться без любых специальных устройств. Они имеют название свободные оси вращения
На расстоянии R от оси горизонтально расположенного диска находится тело, коэффициент трения которого о диск равен k. Диск вращается с угловой скоростью ω.
На тело действуют три силы:
сила тяжести m , сила реакции опоры и сила трения тр.
В инерциальной системе отсчета, связанной с Землей, второй закон Ньютона
будет иметь вид:![]()
Движение тела относительно Земли представляет собой движение в горизонтальной плоскости по окружности радиусом R. Силы, действующие на него в вертикальном направлении, скомпенсированы. Вектор ускорения лежит в горизонтальной плоскости, а само ускорение является центростремительным. Его величина определяется формулой:
Проецирование векторного уравнения на координатные оси X и Y дает два скалярных уравнения:
Первое уравнение показывает, что в роли центростремительной силы выступает сила трения, второе констатирует, что вертикальные силы взаимно уравновешены.
Сила трения покоя подчиняется неравенству:
поэтому при
