Презентация на тему "многогранные углы". Трехгранный и многогранный углы

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

В планиметрии одним из объектов изучения является угол.

Угол - это геометрическая фигура, состоящая из точки - вершины угла и двух лучей, исходящих из этой точки.

Два угла одна сторона, которых общая и две другие являются продолжением одна другой, в планиметрии называются смежными.

Циркуль можно рассматривать как модель плоского угла.

Вспомним понятие двухгранного угла.

Это фигура, образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости в геометрии называется двугранным углом. Полуплоскости - это грани двугранного угла. Прямая а - это ребро двугранного угла.

Крыша дома наглядно демонстрирует двухгранный угол.

Но крыша дома на рисунке два выполнена в виде фигуры образованной из шести плоских углов с общей вершиной так, что углы берутся в определенном порядке и каждая пара соседних углов, включая первый и последний, имеет общую сторону. Как называется такая форма крыши?

В геометрии фигура, составленная из углов

А углы из которых составлен этот угол называются плоскими углами. Стороны плоских углов называются ребрами многогранного угла. Точка О называется вершиной угла.

Примеры многогранных углов можно найти в тетраэдре и параллелепипеде.

Грани тетраэдра DBA, ABC, DBC образуют многогранный угол ВADC. Чаще он называется трёхгранным углом.

В параллелепипеде грани АА1D1D, ABCD, AA1B1B образую трехгранный угол AA1DB.

Ну а крыша дома выполнена в форме шестигранного угла. Она состоит из шести плоских углов.

Для многогранного угла справедлив ряд свойств. Сформулируем их и докажем. Здесь говорится, что утверждение

Во-первых, для любого выпуклого многогранного угла существует плоскость, пересекающая все его рёбра.

Рассмотри для доказательства многогранный угол ОА1А2 А3…Аn.

По условию он выпуклый. Угол называется выпуклым, если он лежит по одну сторону от плоскости каждого из своих плоских углов.

Так как по условию этот угол выпуклый, то точки О, А1, А2 ,А3, Аn лежат по одну сторону от плоскости ОА1А2

Проведем среднюю линию KM треугольника ОА1А2 и выберем из ребер ОА3, ОА4, ОАn то ребро которое образует с плоскостью ОКМ, наименьший двугранный угол. Пусть это будет ребро ОАi.(оа итое)

Рассмотрим полуплоскость α с границей КМ, делящую двугранный угол ОКМАi на два двухгранных угла. Все вершины от А до Аn лежат по одну сторону от плоскости α, а точка О по другую сторону. Следовательно, плоскость α пересекает все ребра многогранного угла. Утверждение доказано.

Выпуклые многогранные углы обладают ещё одним важным свойством.

Сумма плоских углов выпуклого многогранного угла меньше 360°.

Рассмотрим выпуклый многогранный угол с вершиной в точке О. В силу доказанного утверждения существует плоскость, которая пересекает все его ребра.

Проведем такую плоскость α, пусть она пересекает рёбра угла в точках А1, А2, А3 и так далее Аn.

Плоскость α от внешней области плоского угла будет отсекать треугольник. Сумма углов которого 180°. Получим, что сумма всех плоских углов от А1ОА2 до АnОА1 равна выражению преобразуем, данное выражение перегруппируем слагаемые, получим

В данном выражении суммы указанные в скобках, являются суммами плоских углов трехгранного угла, а как известно они больше третьего плоского угла.

Данное неравенство можно записать для всех трёхгранных углов образующих данный многогранный угол.

Следовательно, получим следующее продолжение равенства

Полученный ответ доказывает, что сумма плоских углов выпуклого многогранного угла меньше 360 градусов.

Многогранные углы Многогранный угол является пространственным аналогом многоугольника на плоскости. Напомним, что многоугольником на плоскости называется фигура, образованная простой замкнутой ломаной этой плоскости и ограниченной ею внутренней областью.

Определение многогранного угла Поверхность, образованную конечным набором плоских углов A 1 SA 2, A 2 SA 3, …, An-1 SAn, An. SA 1 с общей вершиной S, в которых соседние углы не имеют общий точек, кроме точек общего луча, а не соседние углы не имеют общих точек, кроме общей вершины, будем называть многогранной поверхностью. Фигура, образованная указанной поверхностью и одной из двух частей пространства, ею ограниченных, называется многогранным углом. Общая вершина S называется вершиной многогранного угла. Лучи SA 1, …, SAn называются ребрами многогранного угла, а сами плоские углы A 1 SA 2, A 2 SA 3, …, An-1 SAn, An. SA 1 – гранями многогранного угла. Многогранный угол обозначается буквами SA 1…An, указывающими вершину и точки на его ребрах.

Виды многогранных углов В зависимости от числа граней многогранные углы бывают трехгранными, четырехгранными, пятигранными и т. д.

Упражнение 1 Приведите примеры многогранников, у которых грани, пересекаясь в вершинах, образуют только: а) трехгранные углы; б) четырехгранные углы; в) пятигранные углы. Ответ: а) Тетраэдр, куб, додекаэдр; б) октаэдр; в) икосаэдр.

Упражнение 2 Приведите примеры многогранников, у которых грани, пересекаясь в вершинах, образуют только: а) трехгранные и четырехгранные углы; б) трехгранные и пятигранные углы; в) четырехгранные и пятигранные углы. Ответ: а) четырехугольная пирамида, треугольная бипирамида; б) пятиугольная пирамида; в) пятиугольная бипирамида.

Неравенство треугольника Для треугольника имеет место следующая теорема. Теорема (Неравенство треугольника). Каждая сторона треугольника меньше суммы двух других сторон. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Всякий плоский угол трехгранного угла меньше суммы двух других его плоских углов.

Доказательство Рассмотрим трехгранный угол SABC. Пусть наибольший из его плоских углов есть угол ASC. Тогда выполняются неравенства ASB ASC

Точка пересечения биссектрис Для треугольника имеет место следующая теорема. Теорема. Биссектрисы треугольника пересекаются в одной точке – центре вписанной окружности. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Биссектральные плоскости двугранных углов трехгранного угла пересекаются по одной прямой.

Доказательство Рассмотрим трехгранный угол SABC. Биссектральная плоскость SAD двугранного угла SA является геометрическим местом точек этого угла, равноудаленных от его граней SAB и SAC. Аналогично, биссектральная плоскость SBE двугранного угла SB является геометрическим местом точек этого угла, равноудаленных от его граней SAB и SBC. Линия их пересечения SO будет состоять из точек, равноудаленных от всех граней трехгранного угла. Следовательно, через нее будет проходить биссектральная плоскость двугранного угла SC.

Точка пересечения серединных перпендикуляров Для треугольника имеет место следующая теорема. Теорема. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке – центре описанной окружности. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Плоскости, проходящие через биссектрисы граней трехгранного угла и перпендикулярные этим граням, пересекаются по одной прямой.

Доказательство Рассмотрим трехгранный угол SABC. Плоскость, проходящая через биссектрису SD угла BSC и перпендикулярная его плоскости, состоит из точек равноудаленных от ребер SB и SC трехгранного угла SABC. Аналогично, плоскость, проходящая через биссектрису SE угла ASC и перпендикулярная его плоскости, состоит из точек равноудаленных от ребер SA и SC трехгранного угла SABC. Линия их пересечения SO будет состоять из точек, равноудаленных от всех ребер трехгранного угла. Следовательно, ее будет содержать плоскость, проходящая через биссектрису угла ASB и перпендикулярная его плоскости.

Точка пересечения медиан Для треугольника имеет место следующая теорема. Теорема. Медианы треугольника пересекаются в одной точке – центре вписанной окружности. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Плоскости, проходящие через ребра трехгранного угла и биссектрисы противоположных граней, пересекаются по одной прямой.

Доказательство Рассмотрим трехгранный угол SABC. На его ребрах отложим равные отрезки SA = SB = CS. Биссектрисы SD, SE, SF плоских углов трехгранного угла являются медианами треугольников соответственно SBC, SAB. Следовательно, AD, BE, CF – медианы треугольника ABC. Пусть O – точка пересечения медиан. Тогда прямая SO будет линией пересечения рассматриваемых плоскостей.

Точка пересечения высот Для треугольника имеет место следующая теорема. Теорема. Высоты треугольника или их продолжения пересекаются в одной точке. Докажем, что для трехгранного угла имеет место следующий пространственный аналог этой теоремы. Теорема. Плоскости, проходящие через ребра трехгранного угла и перпендикулярные плоскостям противоположных граней, пересекаются по одной прямой.

Доказательство Рассмотрим трехгранный угол Sabc. Пусть d, e, f – линии пересечения плоскостей граней трехгранного угла с плоскостями, проходящими через ребра a, b, c этого угла и перпендикулярные соответствующим плоскостям граней. Выберем какую-нибудь точку C на ребре с. Опустим из нее перпендикуляры CD и CE на прямые d и e соответственно. Обозначим A и B точки пересечения прямых CD и CE с прямыми SB и SA соответственно. Прямая d является ортогональной проекцией прямой AD на плоскость BSC. Так как BC перпендикулярна прямой d, то она перпендикулярна и прямой AD. Аналогично, прямая AC перпендикулярна прямой BE. Пусть O – точка пересечения прямых AD и BE. Прямая BC перпендикулярна плоскости SAD, следовательно, она перпендикулярна прямой SO. Аналогично, Прямая AC перпендикулярна плоскости SBE, следовательно, она перпендикулярна прямой SO. Таким образом, прямая SO перпендикулярна прямым BC и AC, следовательно, перпендикулярна плоскости ABC, значит, перпендикулярна и прямой AB. С другой стороны, прямая CO перпендикулярна прямой AB. Таким образом, прямая AB перпендикулярна плоскости SOC. Плоскость SAB проходит через прямую AB, перпендикулярную плоскости SOC, следовательно, сама перпендикулярна этой плоскости. Значит, все три рассматриваемые плоскости пересекаются по прямой SO.

Сумма плоских углов Теорема. Сумма плоских углов трехгранного угла меньше 360°. Доказательство. Пусть SABC – данный трехгранный угол. Рассмотрим трехгранный угол с вершиной A, образованный гранями ABS, ACS и углом BAC. В силу неравенства треугольника, имеет место неравенство BAС

Выпуклые многогранные углы Многогранный угол называется выпуклым, если он является выпуклой фигурой, т. е. вместе с любыми двумя своими точками целиком содержит и соединяющий их отрезок. На рисунке приведены примеры выпуклого и невыпуклого многогранных углов. Свойство. Сумма всех плоских углов выпуклого многогранного угла меньше 360°. Доказательство аналогично доказательству соответствующего свойства для трехгранного угла.
Упражнение 5 Два плоских угла трехгранного угла равны 70° и 80°. В каких границах находится третий плоский угол? Ответ: 10 о

Упражнение 6 Плоские углы трехгранного угла равны 45°, 45° и 60°. Найдите величину угла между плоскостями плоских углов в 45°. Ответ: 90 о.

Упражнение 7 В трехгранном угле два плоских угла равны по 45°; двугранный угол между ними прямой. Найдите третий плоский угол. Ответ: 60 о.

Упражнение 8 Плоские углы трехгранного угла равны 60°, 60° и 90°. На его ребрах от вершины отложены равные отрезки OA, OB, OC. Найдите двугранный угол между плоскостью угла в 90° и плоскостью ABC. Ответ: 90 о.

Упражнение 9 Каждый плоский угол трехгранного угла равен 60°. На одном из его ребер отложен от вершины отрезок, равный 3 см, и из его конца опущен перпендикуляр на противоположную грань. Найдите длину этого перпендикуляра. Ответ: см.

МАОУ «Лицей инновационных технологий»

Многогранные углы. Выпуклые многогранники

Подготовил ученик 10Б класса: Бурыкин Алексей

Проверил: Дубинская И.А.

Хабаровск

Многогранный угол

Многогранным углом называется фигура, образованная плоскими углами так, что выполняются условия:

1)никакие два угла не имеют общих точек, кроме их общей вершины или целой стороны;

2) у каждого из этих углов каждая его сторона является общей с одним и только одним другим таким углом;

3) от каждого угла к каждому можно перейти по углам, имеющим общую сторону;

4) никакие два угла с общей стороной не лежат в одной плоскости.

• Углы ASB, BSC,... называются плоскими углами или гранями , стороны их SA, SB, ... называются рeбрами , а общая вершина S- вершиной многогранного угла.

Теорема1.

В трёхгранном угле каждый плоский угол меньше суммы двух других плоских углов.

Следствие

• / ASC - / ASB / CSB; / ASC - / CSB / ASB.

В трёхгранном угле каждый плоский угол больше разности двух других углов .

Теорема2.

• Сумма величин всех трех плоских углов трехгранного угла меньше 360° .

Доказательство

Обозначим,

тогда из треугольников ASC, ASB, BSC имеем

Теперь неравенство принимает вид

180° - α + 180° - β + 180° - γ 180°,

откуда и следует, что

α + β + γ

Простейшие случаи равенства трёхгранных углов

• 1) по равному двугранному углу, заключённому между двумя соответственно равными и одинаково расположенными плоскими углами , или 2) по равному плоскому углу, заключённому между двумя соответственно равными и одинаково расположенными двугранными углами .

Выпуклый многогранный угол

• Многогранный угол называется выпуклым, если он весь расположен по одну сторону от плоскости каждой из его граней, неограниченно продолженной.

Многогранник.

Многогранник , в трехмерном пространстве- совокупность конечного числа плоских многоугольников, такая, что каждая сторона любого из многоугольников есть одновременно сторона другого, называемого смежным с первым.

Выпуклые многогранники

Многогранник называется выпуклым , если он весь лежит по одну сторону от плоскости любой его грани; тогда грани его тоже выпуклы.

Выпуклый многогранник разрезает пространство на две части – внешнюю и внутреннюю. Внутренняя его часть есть выпуклое тело. Обратно, если поверхность выпуклого тела многогранна, то соответствующий многогранник –выпуклый.

Теорема. Сумма всех плоских углов выпуклого многогранного угла меньше 360 градусов.

Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.

Свойство2. Всякий выпуклый многогранник может быть составлен из пирамид с общей вершиной, основание которых образует поверхность многогранника.

Двугранным углом называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой. Полуплоскости называются гранями, а ограничивающая их прямая - ребром двугранного угла.

На рисунке 142 изображен двугранный угол с ребром а и гранями а и (3.

Плоскость, перпендикулярная ребру двугранного угла, пересекает его грани по двум полупрямым. Угол, образованный этими полупрямыми, называется линейным углом двугранного угла. За меру двугранного угла принимается мера соответствующего ему линейного угла. Если через точку А ребра а двугранного угла провести плоскость у, перпендикулярную этому ребру, то она пересечет плоскости а и (3 по полупрямым (рис. 142); линейный угол данного двугранного угла. Градусная мера этого линейного угла является градусной мерой двугранного угла. Мера двугранного угла не зависит от выбора линейного угла.

Трехгранным углом называется фигура, составленная из трех плоских углов (рис. 143). Эти углы называются гранями трехгранного угла, а их стороны - ребрами. Общая вершина плоских углов называется вершиной трехгранного угла. Двугранные углы, образуемые гранями и их продолжениями, называются двугранными углами трехгранного угла.

Аналогично определяется понятие многогранного угла как фигуры, составленной из плоских углов (рис. 144). Для многогранного угла определяются понятия граней, ребер и двугранных углов так же, как и для трехгранного угла.

Многогранником называют тело, поверхность которого состоит из конечного числа плоских многоугольников (рис. 145).

Многогранник называется выпуклым, если он расположен по одну сторону плоскости каждого многоугольника на его поверхности (рис. 145, а, б). Общая часть такой плоскости и поверхности выпуклого многогранника называется гранью. Грани выпуклого многогранника - выпуклые многоугольники. Стороны граней называются ребрами многогранника, а вершины - вершинами многогранника.

МНОГОГРАННЫЕ УГЛЫ

Многогранный угол является пространственным аналогом многоугольника. Напомним, что многоугольником на плоскости называется фигура, образованная простой замкнутой ломаной и ограниченной ею внутренней областью. Будем считать аналогом точки на плоскости луч в пространстве и аналогом отрезка на плоскости плоский угол в пространстве. Тогда аналогом простой замкнутой ломаной на плоскости является поверхность, образованная конечным набором плоских углов A 1 SA 2 , A 2 SA 3 , …, A n -1 SA n , A n SA 1 с общей вершиной S (рис. 1), в которых соседние углы не имеют общий точек, кроме точек общего луча, а несоседние углы не имеют общих точек, кроме общей вершины. Фигура, образованная указанной поверхностью и одной из двух частей пространства, ею ограниченных, называется многогранным углом . Общая вершина S называется вершиной многогранного угла. Лучи SA 1 , …, SA n называются ребрами многогранного угла, а сами плоские углы A 1 SA 2 , A 2 SA 3 , …, A n -1 SA n , A n SA 1 – гранями многогранного угла. Многогранный угол обозначается буквами SA 1 … A n , указывающими вершину и точки на его ребрах. В зависимости от числа граней многогранные углы называются трехгранными, четырехгранными, пятигранными (рис. 2) и т. д.

Многогранный угол называется выпуклым , если он является выпуклой фигурой, т.е. вместе с любыми двумя своими точками содержит и соединяющий их отрезок. На рисунке 2 трехгранный и четырехгранный углы выпуклые, а пятигранный угол – нет.
Рассмотрим некоторые свойства треугольников и аналогичные им свойства трехгранных углов.
Свойство 1 (Неравенство треугольника). Каждая сторона треугольника меньше суммы двух других его сторон.
Аналогичным свойством для трехгранных углов является следующее свойство.
Свойство 1 ". Каждый плоский угол трехгранного угла меньше суммы двух других его плоских углов.
Доказательство. Рассмотрим трехгранный угол SABC . Пусть наибольший из его плоских углов есть угол ASC . Тогда выполняются неравенства

ASB ASC < ASC + BSC ;BSC ASC < ASC + ASB .

Таким образом, остается доказать неравенство ASС < ASB + BSC .
Отложим на грани ASC угол ASD , равный ASB , и точку B выберем так, чтобы SB = SD (рис. 3). Тогда треугольники ASB и ASD равны (по двум сторонам и углу между ними) и, следовательно, AB = AD . Воспользуемся неравенством треугольника AC < AB + BC . Вычитая из обеих его частей AD = AB , получим неравенство DC < BC. В треугольниках DSC и BSC одна сторона общая (SC ), SD = SB и DC < BC. В этом случае против большей стороны лежит больший угол и, следовательно, DSC < BSC . Прибавляя к обеим частям этого неравенства угол ASD , равный ASB , получим требуемое неравенство ASС < ASB + BSC .

Следствие 1. Сумма плоских углов трехгранного угла меньше 360 ° .
Доказательство. Пусть SABC – данный трехгранный угол. Рассмотрим трехгранный угол с вершиной A , образованный гранями ABS, ACS и углом BAC . В силу доказанного свойства, имеет место неравенство BAС < BAS + CAS . Аналогично, для трехгранных углов с вершинами B и С имеют место неравенства: ABС < ABS + CBS , ACB < ACS + BCS . Складывая эти неравенства и учитывая, что сумма углов треугольника ABC равна 180 ° , получаем 180 ° < BAS +CAS + ABS + CBS +BCS + ACS = 180 ° - ASB + 180 ° - BSC + 180 ° - ASC . Следовательно, ASB + BSC + ASC < 360 ° .
Следствие 2. Сумма плоских углов выпуклого многогранного угла меньше 360.
Доказательство аналогично предыдущему.
Следствие 3. Сумма двугранных углов трехгранного угла больше 180 ° .
Доказательство. Пусть SABC – трехгранный угол. Выберем какую-нибудь точку P внутри него и опустим из нее перпендикуляры PA 1 , PB 1 , PC 1 на грани (рис. 4).

Плоские углы B 1 PC 1 , A 1 PC 1 , A 1 PB 1 дополняют соответствующие двугранные углы с ребрами SA, SB, SC до 180 ° . Следовательно, сумма этих двугранных углов равна 540 ° - (B 1 PC 1 +A 1 PC 1 + A 1 PB 1 ). Учитывая, что сумма плоских углов трехгранного с вершиной P угла меньше 360 ° , получаем, что сумма двугранных углов исходного трехгранного угла больше 180 ° .
Свойство 2. Биссектрисы треугольника пересекаются в одной точке.
Свойство 2". Биссектральные плоскости двугранных углов трехгранного угла пересекаются по одной прямой.
Доказательство аналогично плоскому случаю. А именно, пусть SABC – трехгранный угол. Биссектральная плоскость двугранного угла SA является ГМТ угла, равноудаленных от его граней ASC и ASB . Аналогично, биссектральная плоскость двугранного угла SB является ГМТ угла, равноудаленных от его граней BSA и BSC . Линия их пересечения SO будет равноудалена от всех граней трехгранного угла и, следовательно, через нее будет проходить биссектральная плоскость двугранного угла SC .
Свойство 3. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Свойство 3". Плоскости, проходящие через биссектрисы граней трехгранного угла и перпендикулярные этим граням, пересекаются по одной прямой.
Доказательство аналогично доказательству предыдущего свойства.
Свойство 4. Медианы треугольника пересекаются в одной точке.
Свойство 4". Плоскости, проходящие через ребра трехгранного угла и биссектрисы противоположных граней пересекаются по одной прямой.
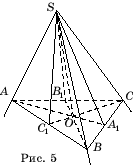
Доказательство. Рассмотрим трехгранный угол SABC, SA = SB = SC (рис. 5). Тогда биссектрисы SA 1 , SB 1 , SC 1 углов BSC, ASC, ASB являются медианами соответствующих треугольников. Поэтому AA 1 , BB 1 , CC 1 – медианы треугольника ABC . Пусть O – точка их пересечения. Прямая SO содержится во всех трех рассматриваемых плоскостях и, следовательно, является линией их пересечения.

Свойство 5. Высоты треугольника пересекаются в одной точке.
Свойство 5 ". Плоскости, проходящие через ребра трехгранного угла и перпендикулярные противоположным граням, пересекаются по одной прямой.
Доказательство. Рассмотрим трехгранный угол с вершиной S и ребрами a, b, c. Обозначим a 1 , b 1 , c 1 – линии пересечения граней с плоскостями, проходящими через соответствующие ребра и перпендикулярные этим граням (рис. 6). Зафиксируем точку C на ребре c и опустим из нее перпендикуляры CA 1 и CB 1 на прямые a 1 и b 1 . Обозначим A и B пересечения прямых CA 1 и CB 1 с прямыми a и b . Тогда SA 1 является проекцией AA 1 на грань BSC . Так как BC перпендикулярна SA 1 , то она перпендикулярна и AA 1 . Аналогично, AC перпендикулярна BB 1 . Таким образом, AA 1 и BB 1 являются высотами треугольника ABC . Пусть O – точка их пересечения. Плоскости, проходящие через прямые a и a 1 , b и b 1 перпендикулярны плоскости ABC и, следовательно, линия их пересечения SO перпендикулярна ABC . Значит, SO перпендикулярна AB . С другой стороны, CO перпендикулярна AB . Поэтому плоскость, проходящая через ребро c и SO будет перпендикулярна противоположной грани.
Свойство 6 (теорема синусов). В треугольнике ABC со сторонами a, b, c соответственно, имеют место равенства a : sin A = b : sin B = c : sin C.
Свойство 6". Пусть a , b , g - плоские углы трехгранного угла, a, b, c – противолежащие им двугранные углы. Тогда sin a : sin a = sin b : sin b = sin g : sin c .
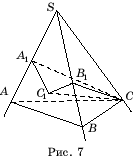
Доказательство. Пусть SABC – трехгранный угол. Опустим из точки C перпендикуляр CC 1 на плоскость ASB и перпендикуляр CA 1 на ребро SA (рис. 7). Тогда угол CA 1 C 1 будет линейным углом двугранного угла a . Поэтому CC 1 = CA 1 sin a = SC sin b sin a. Аналогично показывается, что CC 1 = CB 1 sin b = SC sin a sin b. Следовательно, имеет место равенство sin b sin a = sin a sin b и, значит, равенство sin a : sin a = sin b : sin b . Аналогичным образом доказывается, что имеет место равенство sin b : sin b = sin g : sin c .

Свойство 7. Если в выпуклый четырехугольник можно вписать окружность, то суммы противоположных сторон равны.
Свойство 7". Если в выпуклый четырехгранный угол можно вписать сферу, то суммы противоположных плоских углов равны.

Литература
1. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.
2. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949.
3. Энциклопедия элементарной математики. Книга IV. Геометрия. - М.; 1963.
4. Смирнова И.М. В мире многогранников. – М.: Просвещение, 1995.