Алгоритм решения рациональных уравнений. Построение проекта выхода из затруднения
Урок – практикум по алгебре в 8 классе «Решение дробных рациональных уравнений»
Цели урока:
образовательная – повторение, обобщение и систематизация материала темы; совершенствование графической культуры; контроль усвоения знаний и умений.
развивающая - развитие математического и общего кругозора, внимания, умений сравнивать, классифицировать, проводить анализ и самоанализ.
воспитательная - воспитание интереса к математике, ее истории и приложениям; воспитание активности, общей культуры.
Оборудование: м/медиапроектор, презентация, ПК, «Историческое сообщение», опорные конспекты-задания, таблицы-заготовки с графиками на доске.
Мотивационно - ориентировочный этап
Актуализация знаний
Из предложенных заданий на доске выберите те, которые позволяют повторить:
а) допустимые значения переменной;
б) выделение полного квадрата двучлена;
в) расположение в системе координат графика пропорциональности;
г) вертикальные и горизонтальные асимптоты графика функции;
д) способы решения дробных рациональных уравнений (способы записать на доске, когда дети их назовут):
1) графический;
2) с помощью пропорции – по основному свойству пропорции;
3) преобразование уравнения с использованием условия равенства дроби нулю;
4) условие равенства дробей, у которых одинаковые знаменатели.
Задания на слайде (устная работа)
1. При каких значениях переменной существует данная дробь
а)
б)
 ?
?
2. Разложите на множители
а) 16x 2 +8xy+y 2 б) x 2 -6x+9
3. Каково расположение графиков функций в системе координат и чем оно определяется
а)
 б)
б)

4. Решите уравнение
а)
 б)
б)

5. Составьте задачу по рисунку и уравнение:

6. Проведите классификацию уравнений по способам решения
а) х 2 – 11х + 30 = 0;
б). 8х 2 - 7х = 0;
в). х 2 - 4 = 0;
г). х(4х + 9) = 0.;
д)
 ;
;
е)
 ;
;
ж)
 ;
;
II . Основной этап
а) Тренировочные задания (5 человек у доски, остальные в тетради, фронтальная проверка)
Решить на два варианта с «тихим» контролем у доски (графики заготовить).
|
Вариант 1 1. Решить графически уравнение
|
Вариант 2 Решить графически уравнение
Ответ: -3; 2 |
|
2. Решить уравнение
|
2.
Решить уравнение
|
|
|
Ответ: любое число, кроме 0. |
Ответ: любое число, кроме 0. |
|
б) Исторический материал об Омаре Хайяме . (Приложение 3)
Задача. Решить уравнение.

Ешение х
 ,
где
,
где
 ,
,

в) Дифференцированная работа по группам с элементами самоконтроля на 3 варианта- по уровням.
Я предлагаю вам побывать в роли учителя математики и откорректировать предложенные вам решения уравнений, причем задание у всех разное. Не забудьте отметить выполнение на опорном конспекте по уроку.
Самопроверка по решению у доски (3 ученика)- от каждой группы выходит 1 человек
III.ФИЗМИНУТКА
Упражнения для глаз с использованием геометрических фигур, расположенных на стене классной комнаты.
Цель: расширение зрительной активности, снятие утомления на уроке.
На листе ватмана изображаются различные цветные фигуры (квадрат, круг, ромб и.т.д.), вырезаются и размещаются на стене в кабинете.
Во время физминутки дается задание последовательно перемещать взгляд с одной фигуры на другую (самостоятельно) или по названию фигуры (цвета) учителем. Упражнение можно выполнять сидя и стоя.

Упражнения: «8», «знак бесконечности», «геометрическая зарядка».
Цель: снятие зрительного напряжения.
Задание 1: нарисуйте движениями глаз на доске цифру 8 .
Задание 2: нарисуйте движениями глаз на доске знак бесконечности ∞ .
Данное упражнение можно разнообразить в виде стихотворной инструкции:
Нарисуй
глазами треугольник.
Теперь его
переверни вершиной вниз.
И вновь
глазами ты по периметру веди.
Рисуй
восьмерку вертикально.
Ты головою не
крути,
А лишь глазами осторожно
Ты
вдоль по линиям води.
И на бочок ее
клади.
Теперь следи горизонтально,
И
в центре ты остановись.
Зажмурься
крепко, не ленись.
Глаза открываем мы,
наконец.
Зарядка окончилась. Ты –
молодец
IV.ТВОРЧЕСКАЯ работа в парах: Нарисовать условие задачи, составить уравнение к задаче:
|
1. Расстояние между городами скорый поезд, идущий со скоростью 90 км/ч, проходит на 1,5 ч быстрее товарного, который идет со скоростью 60 км/ч. Каково расстояние между городами. |
|
2. Катер прошел 40 км по течению реки и 6 км против течения, затратив на весь путь 3 ч. Какова собственная скорость катера, если скорость течения реки 3 км/ч? |
|
3. Моторная лодка, скорость которой в стоячей воде 15 км/ч, прошла по течению реки 35 км, а против течения 25 км. На путь по течению реки она затратила столько же времени, сколько на путь против течения. Какова скорость течения реки? |
|
5. Турист проплыл на лодке против течения реки 6 км и по озеру 15 км, затратив на путь по озеру на 1 ч больше, чем на путь по реке. Зная, что скорость течения реки равна 2 км/ч, найти скорость лодки при движении по озеру. |
|
6. Катер, развивающий в стоячей воде скорость 20 км/ч, прошел 36 км против течения и 22 км по течению, затратив на весь путь 3 ч. Найти скорость течения реки. |
|
7. Моторная лодка курсирует между двумя пристанями, расстояние между которыми по реке равно 4 км. На путь по течению у нее уходит на 3 мин меньше, чем на путь против течения. Чему равна скорость течения реки, если известно, что скорость лодки в стоячей воде равна 18 км/ч? |
V.Закрепление изученного
А)№695 (а)- у доски с развернутым объяснением
Б) Самостоятельная работа в форме теста (2 варианта). Проверка по ключу на слайде.
|
А.
2х + 5 = 3(8 - х); Б.
2.
Даны выражения: 1)
А. 1 и 2; Б. 1 и 3; В. только 1; Г. 1, 2 и 3. 3.
Уравнение
А. 13; Б. -2 и 4; В. 13, -2 и 4; Г. нет решений. 4. Расстояние по реке между двумя деревнями равно 2 км. На путь туда и обратно моторная лодка затратила 22 мин. Чему равна собственная скорость лодки, если скорость течения реки равна 1 км/ч? Пусть х км/ч – собственная скорость лодки. Какое из уравнений соответствует условию задачи? А.
2(х + 1) + 2(х – 1) = 22; Б.
Г.
5.
Уравнение
А. 2,5 и -5; Б. 2,5; В. -5 и 5; Г. 5, -5 и 2,5. |
|
1. Какие из уравнений являются дробными рациональными? А. 8х + 24 = 3(8 – х 2); Б. В. Г. 2.
Даны выражения: 1)
А. только 1; Б. только 2; В. 2 и 3; Г. 1, 2 и 3. 3.
Уравнение
А. 1 и 3; Б. -1, -3 и 11; В. 11; Г. нет решений. 4. Моторная лодка курсирует между двумя пристанями, расстояние между которыми по реке равно 4 км. На путь по течению у нее уходит на 3 мин меньше, чем на путь против течения. Чему равна скорость течения реки, если известно, что скорость лодки в стоячей воде равна 18 км/ч? Пусть х км/ч – скорость течения реки. Какое из уравнений соответствует условию задачи? А.
Г. 4(18 + х) – 4(18 – х) = 3. 5.
Уравнение
А. 1 и 2; Б. 1; В. -2 и 2; Г. 2, -2 и 1. |
Ключ к тесту:
|
№ варианта |
|||||
VI.Домашнее задание: №690 (сильным – все, слабым 1 столбик, составить задачу, уравнение к ней и кто смогут -решить по рисунку) ПОДГОТОВИТЬСЯ К ПРОВЕРОЧНОЙ РАБОТЕ
Обратить внимание, что 4 варианта проверочной работы к следующему уроку на ЭЖ.
Закончить предложения с опорного конспекта:
Сегодня на уроке я…
Я понял, что…
Мне бы хотелось…
Я убедился в том, что…
VIII.ОЦЕНИВАНИЕ
ОЦЕНОЧНЫЙ ЛИСТ
|
Затрудняюсь |
|||||
|
Знаю ли я АЛГОРИТМ РЕШЕНИЯ ДРОБНО-РАЦИОНАЛЬНОГО УРАВНЕНИЯ? |
|||||
|
Умею ли я применять его при решении уравнений? |
|||||
|
Смогу ли решать уравнения самостоятельно? |
|||||
|
Как я оцениваю свою работу на уроке : |
|||||
|
Устная работа |
|||||
|
Найди ошибку в уравнении |
|||||
|
Рисунок и уравнение к задаче |
|||||
|
Я ставлю себе за урок |
IX.Дополнительно:
Время интересной задачи: Земной шар опоясали ленточкой по экватору. Затем эту ленточку удлинили на 1 м и равномерно распределяли опять вокруг экватора. Пролезет ли в образовавшийся зазор кошка? /Длина экватора, радиус Земли в справочнике по физике/.
Решение.
Пусть радиус Земли R
см, тогда длина обруча, стягивающего
его экватор, равна С = 2 П R
см. Когда длину обруча увеличили на 1 м
= 100 см, то длина нового обруча оказалась
равной С 1
= 2 П R
+ 100 см, или
С 1
= 2 П R 1
см, где R 1
см - длина радиуса нового обруча. Здесь
предполагается, что зазор на каждом
участке экватора один и тот же и равен
R 1
– R
см.по
формулам корней квадратного уравнения
; овладение навыками решения
рациональных
уравнений
... Урок
-практикум
. На уроке
...
§ 1 Целое и дробное рациональные уравнение
В этом уроке разберем такие понятия, как рациональное уравнение, рациональное выражение, целое выражение, дробное выражение. Рассмотрим решение рациональных уравнений.
Рациональным уравнением называют уравнение, в котором левая и правая части являются рациональными выражениями.
Рациональные выражения бывают:
Дробные.
Целое выражение составлено из чисел, переменных, целых степеней с помощью действий сложения, вычитания, умножения, а также деления на число, отличное от нуля.
Например:
В дробных выражениях есть деление на переменную или выражение с переменной. Например:
Дробное выражение не при всех значениях входящих в него переменных имеет смысл. Например, выражение
при х = -9 не имеет смысла, так как при х = -9 знаменатель обращается в нуль.
Значит, рациональное уравнение может быть целым и дробным.
Целое рациональное уравнение - это рациональное уравнение, в котором левая и правая части - целые выражения.
Например:
![]()
Дробное рациональное уравнение - это рациональное уравнение, в котором или левая, или правая части - дробные выражения.
Например:

§ 2 Решение целого рационального уравнения
Рассмотрим решение целого рационального уравнения.
Например:
Умножим обе части уравнения на наименьший общий знаменатель знаменателей входящих в него дробей.
Для этого:
1. найдем общий знаменатель для знаменателей 2, 3, 6. Он равен 6;
2. найдем дополнительный множитель для каждой дроби. Для этого общий знаменатель 6 делим на каждый знаменатель
дополнительный множитель для дроби
дополнительный множитель для дроби
3. умножим числители дробей на соответствующие им дополнительные множители. Таким образом, получим уравнение
![]()
которое равносильно данному уравнению
Слева раскроем скобки, правую часть перенесем налево, изменив знак слагаемого при переносе на противоположный.
![]()
Приведем подобные члены многочлена и получим
Видим, что уравнение линейное.
Решив его, найдем, что х = 0,5.
§ 3 Решение дробного рационального уравнения
Рассмотрим решение дробного рационального уравнения.
Например:
![]()
1.Умножим обе части уравнения на наименьший общий знаменатель знаменателей входящих в него рациональных дробей.
Найдем общий знаменатель для знаменателей х + 7 и х - 1.
Он равен их произведению (х + 7)(х - 1).
2.Найдем дополнительный множитель для каждой рациональной дроби.
Для этого общий знаменатель (х + 7)(х - 1) делим на каждый знаменатель. Дополнительный множитель для дроби
равен х - 1,
дополнительный множитель для дроби
равен х+7.
3.Умножим числители дробей на соответствующие им дополнительные множители.
Получим уравнение (2х - 1)(х - 1) = (3х + 4)(х + 7), которое равносильно данному уравнению
4.Слева и справа умножим двучлен на двучлен и получим следующее уравнение
5.Правую часть перенесем налево, изменив знак каждого слагаемого при переносе на противоположный:
6.Приведем подобные члены многочлена:
![]()
7.Можно обе части разделить на -1. Получим квадратное уравнение:
![]()
8.Решив его, найдем корни
![]()
Так как в уравнении
левая и правая части - дробные выражения, а в дробных выражениях при некоторых значениях переменных знаменатель может обратиться в нуль, то необходимо проверить, не обращается ли в нуль при найденных х1 и х2 общий знаменатель.
При х = -27 общий знаменатель (х + 7)(х - 1) не обращается в нуль, при х = -1 общий знаменатель также не равен нулю.
Следовательно, оба корня -27 и -1 являются корнями уравнения.
При решении дробного рационального уравнения лучше сразу указать область допустимых значений. Исключить те значения, при которых общий знаменатель обращается в нуль.
Рассмотрим еще один пример решения дробного рационального уравнения.
Например, решим уравнение
![]()
Знаменатель дроби правой части уравнения разложим на множители
![]()
Получим уравнение

Найдем общий знаменатель для знаменателей (х - 5), х, х(х - 5).
Им будет выражение х(х - 5).
теперь найдем область допустимых значений уравнения
Для этого общий знаменатель приравняем к нулю х(х - 5) = 0.
Получим уравнение, решив которое, найдем, что при х = 0 или при х = 5 общий знаменатель обращается в нуль.
Значит, х = 0 или х = 5 не могут быть корнями нашего уравнения.
Теперь можно найти дополнительные множители.
Дополнительным множителем для рациональной дроби
дополнительным множителем для дроби
будет (х - 5),
а дополнительный множитель дроби
Числители умножим на соответствующие дополнительные множители.
Получим уравнение х(х - 3) + 1(х - 5) = 1(х + 5).
Раскроем скобки слева и справа, х2 - 3х + х - 5 = х + 5.
Перенесем слагаемые справа налево, изменив знак переносимых слагаемых:
Х2 - 3х + х - 5 - х - 5 = 0
И после приведения подобных членов получим квадратное уравнение х2 - 3х - 10 = 0. Решив его, найдем корни х1 = -2; х2 = 5.
Но мы уже выяснили, что при х = 5 общий знаменатель х(х - 5) обращается в нуль. Следовательно, корнем нашего уравнения
будет х = -2.
§ 4 Краткие итоги урока
Важно запомнить:
При решении дробных рациональных уравнений надо поступить следующим образом:
1.Найти общий знаменатель дробей входящих в уравнение. При этом если знаменатели дробей можно разложить на множители, то разложить их на множители и затем найти общий знаменатель.
2.Умножить обе части уравнения на общий знаменатель: найти дополнительные множители, умножить числители на дополнительные множители.
3.Решить получившееся целое уравнение.
4.Исключить из его корней те, которые обращают в нуль общий знаменатель.
Список использованной литературы:
- Макарычев Ю.Н., Н. Г. Миндюк, Нешков К.И., Суворова С.Б. / Под редакцией Теляковского С.А. Алгебра: учебн. для 8 кл. общеобразоват. учреждений. - М.: Просвещение, 2013.
- Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учеб. для общеобразоват. учреждений. - М.: Мнемозина.
- Рурукин А.Н. Поурочные разработки по алгебре: 8 класс.- М.: ВАКО, 2010.
- Алгебра 8 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворовой / Авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. -Волгоград: Учитель, 2005.
Муниципальное общеобразовательное учреждение
Средняя общеобразовательная школа №21
Рациональные уравнения.
(8 класс)
Учитель математики:
Квасницкая И.В.
Ковров,
2010-2011
Тема: Рациональные уравнения.
Цель: Формирование навыков решения рациональных уравнений.
Задачи: - формирование понятия «Рациональное уравнение»;
Формирование навыков решения рациональных уравнений различными способами;
Совершенствование навыков преобразования алгебраических дробей;
Совершенствование навыков применения формул сокращенного умножения в преобразовании алгебраических дробей;
Совершенствование навыков устного счета;
Развитие мыслительных операций;
Воспитание грамотной математической речи, аккуратности;
Воспитание сотрудничества, взаимопомощи.
План урока:
1. Самоопределение к учебной деятельности.
2. Актуализация знаний и фиксация затруднения в деятельности.
3. Выявление причины затруднения и постановка цели деятельности.
4. Построение проекта выхода из затруднения.
5. Первичное закрепление во внешней речи.
6. Самостоятельная работа с самопроверкой по эталону.
7. Включение в систему знаний и повторение.
8. Рефлексия деятельности на уроке.
9. Домашнее задание.
Ход урока.
Оборудование, демонстрационный материал:
1) задания для актуализации знаний
№ 1
· ·
·
№2
 +
+ :
: -
-
№ 3
 -2х=
-2х= +
+
№ 4
 =0.
=0.
2) Алгоритм решения уравнений
1) Привести дроби к общему знаменателю в левой и правой частях уравнения.
2) Воспользоваться правилами:
а) равенства дроби нулю;
б) свойствами пропорции;
в) равенства дробей.
3) Алгоритм решения рациональных уравнений
а) равенства дроби нулю;
б) свойствами пропорции;
в) равенства дробей.
4) Задание для первичного закрепления во внешней речи
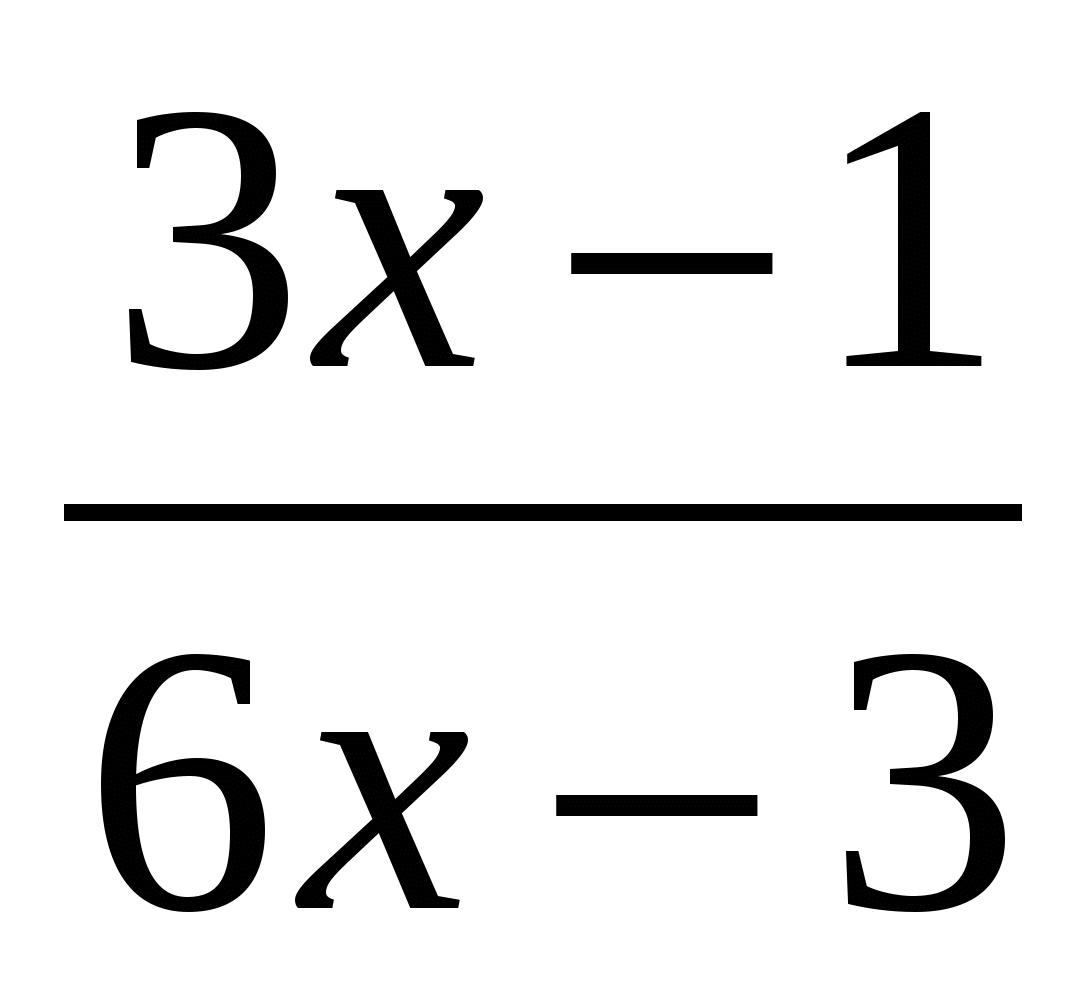 -
- =
=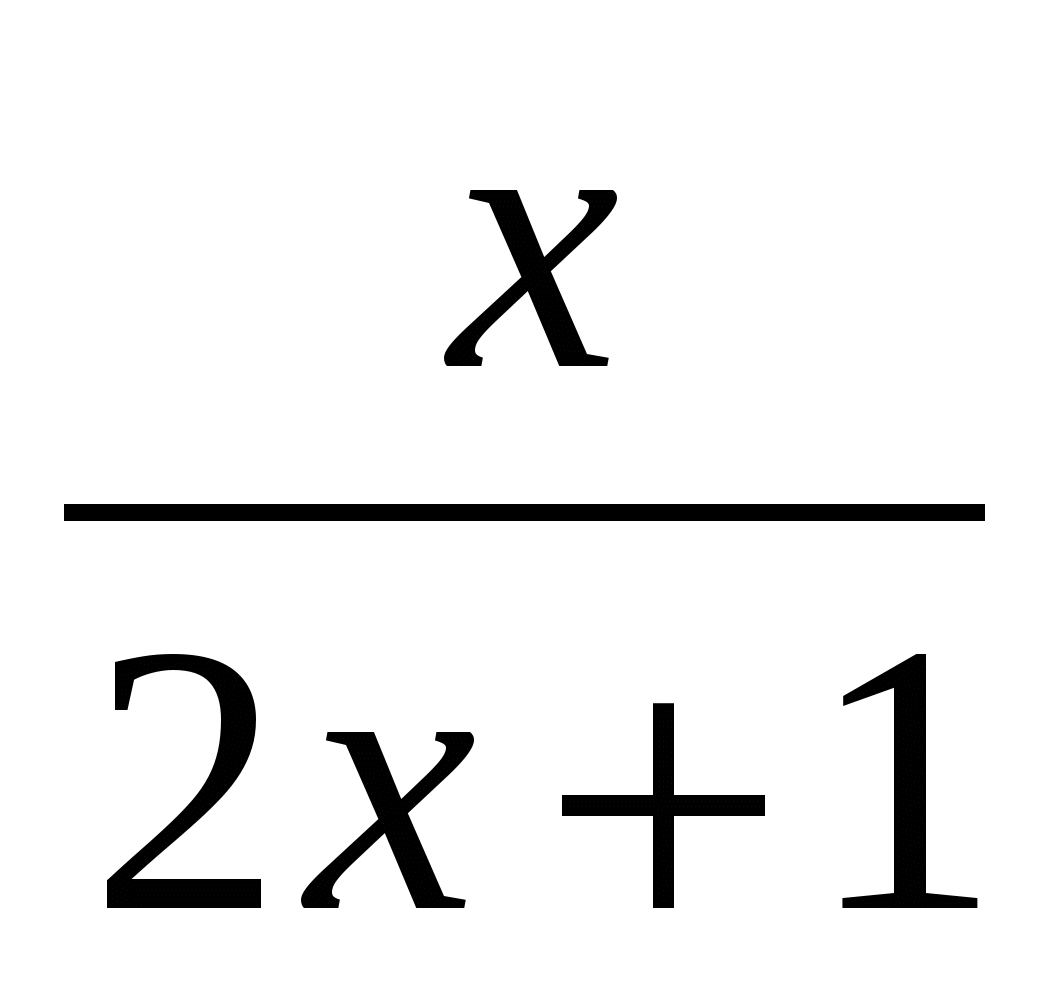 ,
,
 -
- =,
=,
+ =, | ·3(2х-1)(2х+1)
=, | ·3(2х-1)(2х+1)
(2х+1)(3х-1)+3=3(2х-1)х,
6х 2 -2х+3х-1+3=6х 2 -3х,
5) образец выполнения задания в парах
№ 250(б)
 =
= ,
,
О.Д.З.: х≠2,
2- не входит в О.Д.З.
Ответ. Корней нет
6) эталон для самопроверки самостоятельной работы
 +
+ =0,
=0,
О.Д.З.: t ≠1,6; t≠,
 =0,
=0,
 =0,
=0,
46t+46=0,
t=1- входит в О.Д.З.
Ответ. 1.
Ход урока
1. Самоопределение к учебной деятельности
– Здравствуйте! Какую тему мы изучали на прошлых уроках? (Преобразование рациональных выражений.)
– На прошлых уроках вы многому научились, и эти знания помогут сегодня совершить новое «открытие».
2. Актуализация знаний и фиксация затруднения в деятельности
Цель этапа:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: действия с алгебраическими дробями;
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;
4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний: решить рациональное уравнение.
Организация учебного процесса на этапе 2:
1. На доске: ··
От значения каких переменных не зависит значение выражения? Укажите все допустимые значения переменных.
2. На доске: +:-
Назовите порядок действий. Какую формулу сокращенного умножения примените для разложения на множители двучлена, находящегося в знаменателе 1 дроби? В тетради выполните 1-ое действие. (На закрытой доске 1 ученик.)
Итак, какой ответ получился? Все ли получили такой ответ? Какое действие необходимо выполнить вторым? Можно ли выполнить одновременно сложение и вычитание алгебраических дробей? Не повлияет ли это на результат?
Пожалуйста, выполните 2 действие, свой ответ сверьте с ответом на доске. (Работа в парах ).
3. Задание группам. Решите уравнение: -2х=+
Каким алгоритмом пользовались при решении? (формулируют, вывесить на доску. Рассмотреть различные способы решения )
4. - Решите равнение: =0. В чем отличие данного уравнения от предыдущего? (в знаменателе переменная). Знаете способ его решения? (Нет).
3. Выявление причины затруднения и постановка цели деятельности
Цель этапа:
1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;
2) согласовать цель и тему урока.
Организация учебного процесса на этапе 3:
Что собою представляет левая часть данного уравнения? Что собою представляет правая часть данного уравнения? Как называются уравнения такого вида? (Рациональное уравнение)
Тема. Цель. (Ученики формулируют сами. )
Так какое уравнение называют рациональным? (учащиеся формулируют ) Сравните с определением в учебнике.
4. Построение проекта выхода из затруднения
Цель этапа:
1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью алгоритма.
Организация учебного процесса на этапе 4:
Как вы думаете, почему возникло затруднение при решении заданного уравнения? (Не знаем способы его решения.)
Какие предложения у Вас появились? (Воспользоваться свойством равенства нулю дроби: (х-9) не может быть равно нулю, поэтому (2х-10) равно 0, откуда находим х=5.)
Задание группам. Решите уравнение:
= -
-
Каким алгоритмом решения вы пользовались? (что и в начале урока).
Есть ли отличие при решении данного рационального уравнения от того, которое было решено в начале урока? (Да, необходимо помнить о том, что знаменатель дроби не может быть равен нулю, то есть найти область допустимых значений переменной.)
Нужно ли эту особенность внести в алгоритм решения рациональных уравнений? (Конечно.)
- 1) Разложить знаменатель на множители.
2) Найти область допустимых значений переменной.
3) Привести дроби к общему знаменателю в левой и правой частях уравнения.
4) Воспользоваться правилами:
а) равенства дроби нулю;
б) свойствами пропорции;
в) равенства дробей.
Сформулируйте алгоритм решения рациональных уравнений. (Алгоритм вывесить на доску.)
6. Самостоятельная работа с самопроверкой по эталону
Цель этапа:
проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
Организация учебного процесса на этапе 6:
Работы проверяются по эталону. Ошибки исправляются, анализируются, выясняется их причина.
7. Включение в систему знаний и повторение
Цель этапа:
Тренировать навыки использования нового содержания совместно с ранее изученным: решение задач с помощью системы уравнений;
Организация учебного процесса на этапе 7:
№241.(Устно.)
8. Рефлексия деятельности на уроке
Цель этапа:
1) зафиксировать новое содержание, изученное на уроке;
2) оценить собственную деятельность на уроке;
3) поблагодарить одноклассников, которые помогли получить результат урока;
4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;
5) обсудить и записать домашнее задание.
Организация учебного процесса на этапе 8:
– Что нового узнали на уроке?
– Что использовали для «открытия» нового знания?
– Проанализируйте свою работу на уроке.
Домашнее задание
1. Общие положения
1.1. С целью поддержания деловой репутации и обеспечения выполнения норм федерального законодательства ФГАУ ГНИИ ИТТ «Информика» (далее – Компания) считает важнейшей задачей обеспечение легитимности обработки и безопасности персональных данных субъектов в бизнес-процессах Компании.
1.2. Для решения данной задачи в Компании введена, функционирует и проходит периодический пересмотр (контроль) система защиты персональных данных.
1.3. Обработка персональных данных в Компании основана на следующих принципах:
Законности целей и способов обработки персональных данных и добросовестности;
Соответствия целей обработки персональных данных целям, заранее определенным и заявленным при сборе персональных данных, а также полномочиям Компании;
Соответствия объема и характера обрабатываемых персональных данных, способов обработки персональных данных целям обработки персональных данных;
Достоверности персональных данных, их актуальности и достаточности для целей обработки, недопустимости обработки избыточных по отношению к целям сбора персональных данных;
Легитимности организационных и технических мер по обеспечению безопасности персональных данных;
Непрерывности повышения уровня знаний работников Компании в сфере обеспечения безопасности персональных данных при их обработке;
Стремления к постоянному совершенствованию системы защиты персональных данных.
2. Цели обработки персональных данных
2.1. В соответствии с принципами обработки персональных данных, в Компании определены состав и цели обработки.
Цели обработки персональных данных:
Заключение, сопровождение, изменение, расторжение трудовых договоров, которые являются основанием для возникновения или прекращения трудовых отношений между Компанией и ее работниками;
Предоставление портала, сервисов личного кабинета для учеников, родителей и учителей;
Хранение результатов обучения;
Исполнение обязательств, предусмотренных федеральным законодательством и иными нормативными правовыми актами;
3. Правила обработки персональных данных
3.1. В Компании осуществляется обработка только тех персональных данных, которые представлены в утвержденном Перечне персональных данных, обрабатываемых в ФГАУ ГНИИ ИТТ «Информика»
3.2. В Компании не допускается обработка следующих категорий персональных данных:
Расовая принадлежность;
Политические взгляды;
Философские убеждения;
О состоянии здоровья;
Состояние интимной жизни;
Национальная принадлежность;
Религиозные убеждения.
3.3. В Компании не обрабатываются биометрические персональные данные (сведения, которые характеризуют физиологические и биологические особенности человека, на основании которых можно установить его личность).
3.4. В Компании не осуществляется трансграничная передача персональных данных (передача персональных данных на территорию иностранного государства органу власти иностранного государства, иностранному физическому лицу или иностранному юридическому лицу).
3.5. В Компании запрещено принятие решений относительно субъектов персональных данных на основании исключительно автоматизированной обработки их персональных данных.
3.6. В Компании не осуществляется обработка данных о судимости субъектов.
3.7. Компания не размещает персональные данные субъекта в общедоступных источниках без его предварительного согласия.
4. Реализованные требования по обеспечению безопасности персональных данных
4.1. С целью обеспечения безопасности персональных данных при их обработке в Компании реализуются требования следующих нормативных документов РФ в области обработки и обеспечения безопасности персональных данных:
Федеральный закон от 27.07.2006 г. № 152-ФЗ «О персональных данных»;
Постановление Правительства Российской Федерации от 1 ноября 2012 г. N 1119 "Об утверждении требований к защите персональных данных при их обработке в информационных системах персональных данных";
Постановление Правительства Российской Федерации от 15.09.2008 г. №687 «Об утверждении Положения об особенностях обработки персональных данных, осуществляемой без использования средств автоматизации»;
Приказ ФСТЭК России от 18.02.2013 N 21 "Об утверждении Состава и содержания организационных и технических мер по обеспечению безопасности персональных данных при их обработке в информационных системах персональных данных";
Базовая модель угроз безопасности персональных данных при их обработке в информационных системах персональных данных (утверждена заместителем директора ФСТЭК России 15.02.2008 г.);
Методика определения актуальных угроз безопасности персональных данных при их обработке в информационных системах персональных данных (утверждена заместителем директора ФСТЭК России 14.02.2008 г.).
4.2. Компания проводит оценку вреда, который может быть причинен субъектам персональных данных и определяет угрозы безопасности персональных данных. В соответствии с выявленными актуальными угрозами Компания применяет необходимые и достаточные организационные и технические меры, включающие в себя использование средств защиты информации, обнаружение фактов несанкционированного доступа, восстановление персональных данных, установление правил доступа к персональным данным, а также контроль и оценку эффективности применяемых мер.
4.3. В Компании назначены лица, ответственные за организацию обработки и обеспечения безопасности персональных данных.
4.4. Руководство Компании осознает необходимость и заинтересовано в обеспечении должного как с точки зрения требований нормативных документов РФ, так и обоснованного с точки зрения оценки рисков для бизнеса уровня безопасности персональных данных, обрабатываемых в рамках выполнения основной деятельности Компании.
Продолжаем разговор про решение уравнений . В этой статье мы подробно остановимся на рациональных уравнениях и принципах решения рациональных уравнений с одной переменной. Сначала разберемся, уравнения какого вида называются рациональными, дадим определение целых рациональных и дробных рациональных уравнений, приведем примеры. Дальше получим алгоритмы решения рациональных уравнений, и, конечно же, рассмотрим решения характерных примеров со всеми необходимыми пояснениями.
Навигация по странице.
Отталкиваясь от озвученных определений, приведем несколько примеров рациональных уравнений. Например, x=1 , 2·x−12·x 2 ·y·z 3 =0 , , - это все рациональные уравнения.
Из показанных примеров видно, что рациональные уравнения, как, впрочем, и уравнения других видов, могут быть как с одной переменной, так и с двумя, тремя и т.д. переменными. В следующих пунктах мы будем говорить о решении рациональных уравнений с одной переменной. Решение уравнений с двумя переменными и их большим числом заслуживают отдельного внимания.
Помимо деления рациональных уравнений по количеству неизвестных переменных, их еще разделяют на целые и дробные. Дадим соответствующие определения.
Определение.
Рациональное уравнение называют целым , если и левая, и правая его части являются целыми рациональными выражениями.
Определение.
Если хотя бы одна из частей рационального уравнения является дробным выражением, то такое уравнение называется дробно рациональным (или дробным рациональным).
Понятно, что целые уравнения не содержат деления на переменную, напротив, дробные рациональные уравнения обязательно содержат деление на переменную (или переменную в знаменателе). Так 3·x+2=0 и (x+y)·(3·x 2 −1)+x=−y+0,5 – это целые рациональные уравнения, обе их части являются целыми выражениями. А и x:(5·x 3 +y 2)=3:(x−1):5 – примеры дробных рациональных уравнений.
Завершая этот пункт, обратим внимание на то, что известные к этому моменту линейные уравнения и квадратные уравнения являются целыми рациональными уравнениями.
Решение целых уравнений
Одним из основных подходов к решению целых уравнений является их сведение к равносильным алгебраическим уравнениям . Это можно сделать всегда, выполнив следующие равносильные преобразования уравнения :
- сначала выражение из правой части исходного целого уравнения переносят в левую часть с противоположным знаком, чтобы получить нуль в правой части;
- после этого в левой части уравнения образовавшееся стандартного вида.
В результате получается алгебраическое уравнение, которое равносильно исходному целому уравнению. Так в самых простых случаях решение целых уравнений сводятся к решению линейных или квадратных уравнений, а в общем случае – к решению алгебраического уравнения степени n . Для наглядности разберем решение примера.
Пример.
Найдите корни целого уравнения 3·(x+1)·(x−3)=x·(2·x−1)−3 .
Решение.
Сведем решение этого целого уравнения к решению равносильного ему алгебраического уравнения. Для этого, во-первых, перенесем выражение из правой части в левую, в результате приходим к уравнению 3·(x+1)·(x−3)−x·(2·x−1)+3=0 . И, во-вторых, преобразуем выражение, образовавшееся в левой части, в многочлен стандартного вида, выполнив необходимые : 3·(x+1)·(x−3)−x·(2·x−1)+3= (3·x+3)·(x−3)−2·x 2 +x+3= 3·x 2 −9·x+3·x−9−2·x 2 +x+3=x 2 −5·x−6 . Таким образом, решение исходного целого уравнения сводится к решению квадратного уравнения x 2 −5·x−6=0 .
Вычисляем его дискриминант D=(−5) 2 −4·1·(−6)=25+24=49
, он положительный, значит, уравнение имеет два действительных корня, которые находим по формуле корней квадратного уравнения :
Для полной уверенности выполним проверку найденных корней уравнения . Сначала проверяем корень 6 , подставляем его вместо переменной x в исходное целое уравнение: 3·(6+1)·(6−3)=6·(2·6−1)−3 , что то же самое, 63=63 . Это верное числовое равенство, следовательно, x=6 действительно является корнем уравнения. Теперь проверяем корень −1 , имеем 3·(−1+1)·(−1−3)=(−1)·(2·(−1)−1)−3 , откуда, 0=0 . При x=−1 исходное уравнение также обратилось в верное числовое равенство, следовательно, x=−1 тоже является корнем уравнения.
Ответ:
6 , −1 .
Здесь еще нужно заметить, что с представлением целого уравнения в виде алгебраического уравнения связан термин «степень целого уравнения». Дадим соответствующее определение:
Определение.
Степенью целого уравнения называют степень равносильного ему алгебраического уравнения.
Согласно этому определению целое уравнение из предыдущего примера имеет вторую степень.
На этом можно бы было закончить с решением целых рациональных уравнений, если бы ни одно но…. Как известно, решение алгебраических уравнений степени выше второй сопряжено со значительными сложностями, а для уравнений степени выше четвертой вообще не существует общих формул корней. Поэтому для решения целых уравнений третьей, четвертой и более высоких степеней часто приходится прибегать к другим методам решения.
В таких случаях иногда выручает подход к решению целых рациональных уравнений, основанный на методе разложения на множители . При этом придерживаются следующего алгоритма:
- сначала добиваются, чтобы в правой части уравнения был нуль, для этого переносят выражение из правой части целого уравнения в левую;
- затем, полученное выражение в левой части представляют в виде произведения нескольких множителей, что позволяет перейти к совокупности нескольких более простых уравнений.
Приведенный алгоритм решения целого уравнения через разложение на множители требует детального разъяснения на примере.
Пример.
Решите целое уравнение (x 2 −1)·(x 2 −10·x+13)= 2·x·(x 2 −10·x+13) .
Решение.
Сначала как обычно переносим выражение из правой части в левую часть уравнения, не забыв изменить знак, получаем (x 2 −1)·(x 2 −10·x+13)− 2·x·(x 2 −10·x+13)=0 . Здесь достаточно очевидно, что не целесообразно преобразовывать левую часть полученного уравнения в многочлен стандартного вида, так как это даст алгебраическое уравнение четвертой степени вида x 4 −12·x 3 +32·x 2 −16·x−13=0 , решение которого сложно.
С другой стороны, очевидно, что в левой части полученного уравнения можно x 2 −10·x+13 , тем самым представив ее в виде произведения. Имеем (x 2 −10·x+13)·(x 2 −2·x−1)=0 . Полученное уравнение равносильно исходному целому уравнению, и его, в свою очередь, можно заменить совокупностью двух квадратных уравнений x 2 −10·x+13=0 и x 2 −2·x−1=0 . Нахождение их корней по известным формулам корней через дискриминант не составляет труда, корни равны . Они являются искомыми корнями исходного уравнения.
Ответ:
Для решения целых рациональных уравнений также бывает полезен метод введения новой переменной . В некоторых случаях он позволяет переходить к уравнениям, степень которых ниже, чем степень исходного целого уравнения.
Пример.
Найдите действительные корни рационального уравнения (x 2 +3·x+1) 2 +10=−2·(x 2 +3·x−4) .
Решение.
Сведение данного целого рационального уравнения к алгебраическому уравнению является, мягко говоря, не очень хорошей идеей, так как в этом случае мы придем к необходимости решения уравнения четвертой степени, не имеющего рациональных корней. Поэтому, придется поискать другой способ решения.
Здесь несложно заметить, что можно ввести новую переменную y , и заменить ею выражение x 2 +3·x . Такая замена приводит нас к целому уравнению (y+1) 2 +10=−2·(y−4) , которое после переноса выражения −2·(y−4) в левую часть и последующего преобразования образовавшегося там выражения, сводится к квадратному уравнению y 2 +4·y+3=0 . Корни этого уравнения y=−1 и y=−3 легко находятся, например, их можно подобрать, основываясь на теореме, обратной теореме Виета .
Теперь переходим ко второй части метода введения новой переменной, то есть, к проведению обратной замены. Выполнив обратную замену, получаем два уравнения x 2 +3·x=−1 и x 2 +3·x=−3 , которые можно переписать как x 2 +3·x+1=0 и x 2 +3·x+3=0 . По формуле корней квадратного уравнения находим корни первого уравнения . А второе квадратное уравнение не имеет действительных корней, так как его дискриминант отрицателен (D=3 2 −4·3=9−12=−3 ).
Ответ:
Вообще, когда мы имеем дело с целыми уравнениями высоких степеней, всегда надо быть готовым к поиску нестандартного метода или искусственного приема для их решения.
Решение дробно рациональных уравнений
Сначала будет полезно разобраться, как решать дробно рациональные уравнения вида , где p(x) и q(x) – целые рациональные выражения. А дальше мы покажем, как свести решение остальных дробно рациональных уравнений к решению уравнений указанного вида.
В основе одного из подходов к решению уравнения лежит следующее утверждение: числовая дробь u/v , где v – отличное от нуля число (иначе мы столкнемся с , которое не определено), равна нулю тогда и только тогда, когда ее числитель равен нулю, то есть, тогда и только тогда, когда u=0 . В силу этого утверждения, решение уравнения сводится к выполнению двух условий p(x)=0 и q(x)≠0 .
Этому заключению соответствует следующий алгоритм решения дробно рационального уравнения . Чтобы решить дробное рациональное уравнение вида , надо
- решить целое рациональное уравнение p(x)=0 ;
- и проверить, выполняется ли для каждого найденного корня условие q(x)≠0 , при этом
- если выполняется, то этот корень является корнем исходного уравнения;
- если не выполняется, то этот корень – посторонний, то есть, не является корнем исходного уравнения.
Разберем пример применения озвученного алгоритма при решении дробного рационального уравнения.
Пример.
Найдите корни уравнения .
Решение.
Это дробно рациональное уравнение, причем вида , где p(x)=3·x−2 , q(x)=5·x 2 −2=0 .
Согласно алгоритму решения дробно рациональных уравнений этого вида, нам сначала надо решить уравнение 3·x−2=0 . Это линейное уравнение, корнем которого является x=2/3 .
Осталось выполнить проверку для этого корня, то есть проверить, удовлетворяет ли он условию 5·x 2 −2≠0 . Подставляем в выражение 5·x 2 −2 вместо x число 2/3 , получаем . Условие выполнено, поэтому x=2/3 является корнем исходного уравнения.
Ответ:
2/3 .
К решению дробного рационального уравнения можно подходить с немного другой позиции. Это уравнение равносильно целому уравнению p(x)=0 на переменной x исходного уравнения. То есть, можно придерживаться такого алгоритма решения дробно рационального уравнения :
- решить уравнение p(x)=0 ;
- найти ОДЗ переменной x ;
- взять корни, принадлежащие области допустимых значений, - они являются искомыми корнями исходного дробного рационального уравнения.
Для примера решим дробное рациональное уравнение по этому алгоритму.
Пример.
Решите уравнение .
Решение.
Во-первых, решаем квадратное уравнение x 2 −2·x−11=0 . Его корни можно вычислить, используя формулу корней для четного второго коэффициента , имеем D 1 =(−1) 2 −1·(−11)=12 , и .
Во-вторых, находим ОДЗ переменной x для исходного уравнения. Ее составляют все числа, для которых x 2 +3·x≠0 , что то же самое x·(x+3)≠0 , откуда x≠0 , x≠−3 .
Остается проверить, входят ли найденные на первом шаге корни в ОДЗ. Очевидно, да. Следовательно, исходное дробно рациональное уравнение имеет два корня .
Ответ:
Отметим, что такой подход выгоднее первого, если легко находится ОДЗ, и особенно выгоден, если еще при этом корни уравнения p(x)=0 иррациональные, например, , или рациональные, но с довольно большим числителем и/или знаменателем, к примеру, 127/1101 и −31/59 . Это связано с тем, что в таких случаях проверка условия q(x)≠0 потребует значительных вычислительных усилий, и проще исключить посторонние корни по ОДЗ.
В остальных случаях при решении уравнения , особенно когда корни уравнения p(x)=0 целые, выгоднее использовать первый из приведенных алгоритмов. То есть, целесообразно сразу находить корни целого уравнения p(x)=0 , после чего проверять, выполняется ли для них условие q(x)≠0 , а не находить ОДЗ, после чего решать уравнение p(x)=0 на этой ОДЗ. Это связано с тем, что в таких случаях сделать проверку обычно проще, чем найти ОДЗ.
Рассмотрим решение двух примеров для иллюстрации оговоренных нюансов.
Пример.
Найдите корни уравнения .
Решение.
Сначала найдем корни целого уравнения (2·x−1)·(x−6)·(x 2 −5·x+14)·(x+1)=0 , составленного с использованием числителя дроби. Левая часть этого уравнения – произведение, а правая – нуль, поэтому, согласно методу решения уравнений через разложение на множители, это уравнение равносильно совокупности четырех уравнений 2·x−1=0 , x−6=0 , x 2 −5·x+14=0 , x+1=0 . Три из этих уравнений линейные и одно – квадратное, их мы умеем решать. Из первого уравнения находим x=1/2 , из второго – x=6 , из третьего – x=7 , x=−2 , из четвертого – x=−1 .
С найденными корнями достаточно легко выполнить их проверку на предмет того, не обращается ли при них в нуль знаменатель дроби, находящейся в левой части исходного уравнения, а определить ОДЗ, напротив, не так просто, так как для этого придется решать алгебраическое уравнение пятой степени. Поэтому, откажемся от нахождения ОДЗ в пользу проверки корней. Для этого по очереди подставляем их вместо переменной x
в выражение x 5 −15·x 4 +57·x 3 −13·x 2 +26·x+112
, получающихся после подстановки, и сравниваем их с нулем:
(1/2) 5 −15·(1/2) 4 +
57·(1/2) 3 −13·(1/2) 2 +26·(1/2)+112=
1/32−15/16+57/8−13/4+13+112=
122+1/32≠0
;
6 5 −15·6 4 +57·6 3 −13·6 2 +26·6+112=
448≠0
;
7 5 −15·7 4 +57·7 3 −13·7 2 +26·7+112=0
;
(−2) 5 −15·(−2) 4 +57·(−2) 3 −13·(−2) 2 +
26·(−2)+112=−720≠0
;
(−1) 5 −15·(−1) 4 +57·(−1) 3 −13·(−1) 2 +
26·(−1)+112=0
.
Таким образом, 1/2 , 6 и −2 являются искомыми корнями исходного дробно рационального уравнения, а 7 и −1 – посторонние корни.
Ответ:
1/2 , 6 , −2 .
Пример.
Найдите корни дробного рационального уравнения .
Решение.
Сначала найдем корни уравнения (5·x 2 −7·x−1)·(x−2)=0 . Это уравнение равносильно совокупности двух уравнений: квадратного 5·x 2 −7·x−1=0 и линейного x−2=0 . По формуле корней квадратного уравнения находим два корня , а из второго уравнения имеем x=2 .
Проверять, не обращается ли в нуль знаменатель при найденных значениях x , достаточно неприятно. А определить область допустимых значений переменной x в исходном уравнении достаточно просто. Поэтому, будем действовать через ОДЗ.
В нашем случае ОДЗ переменной x исходного дробно рационального уравнения составляют все числа, кроме тех, для которых выполняется условие x 2 +5·x−14=0 . Корнями этого квадратного уравнения являются x=−7 и x=2 , откуда делаем вывод про ОДЗ: ее составляют все такие x , что .
Остается проверить, принадлежат ли найденные корни и x=2 области допустимых значений. Корни - принадлежат, поэтому, они являются корнями исходного уравнения, а x=2 – не принадлежит, поэтому, это посторонний корень.
Ответ:
Еще полезным будет отдельно остановиться на случаях, когда в дробном рациональном уравнении вида в числителе находится число, то есть, когда p(x) представлено каким-либо числом. При этом
- если это число отлично от нуля, то уравнение не имеет корней, так как дробь равна нулю тогда и только тогда, когда ее числитель равен нулю;
- если это число нуль, то корнем уравнения является любое число из ОДЗ.
Пример.
Решение.
Так как в числителе дроби, находящейся в левой части уравнения, отличное от нуля число, то ни при каких x значение этой дроби не может равняться нулю. Следовательно, данное уравнение не имеет корней.
Ответ:
нет корней.
Пример.
Решите уравнение .
Решение.
В числителе дроби, находящейся в левой части данного дробного рационального уравнения, находится нуль, поэтому значение этой дроби равно нулю для любого x , при котором она имеет смысл. Другими словами, решением этого уравнения является любое значение x из ОДЗ этой переменной.
Осталось определить эту область допустимых значений. Она включает все такие значения x , при которых x 4 +5·x 3 ≠0 . Решениями уравнения x 4 +5·x 3 =0 являются 0 и −5 , так как, это уравнение равносильно уравнению x 3 ·(x+5)=0 , а оно в свою очередь равносильно совокупности двух уравнений x 3 =0 и x+5=0 , откуда и видны эти корни. Следовательно, искомой областью допустимых значений являются любые x , кроме x=0 и x=−5 .
Таким образом, дробно рациональное уравнение имеет бесконечно много решений, которыми являются любые числа, кроме нуля и минус пяти.
Ответ:
Наконец, пришло время поговорить о решении дробных рациональных уравнений произвольного вида. Их можно записать как r(x)=s(x) , где r(x) и s(x) – рациональные выражения, причем хотя бы одно из них дробное. Забегая вперед, скажем, что их решение сводится к решению уравнений уже знакомого нам вида .
Известно, что перенос слагаемого из одной части уравнения в другую с противоположным знаком приводит к равносильному уравнению, поэтому уравнению r(x)=s(x) равносильно уравнение r(x)−s(x)=0 .
Также мы знаем, что можно любое , тождественно равную этому выражению. Таким образом, рациональное выражение в левой части уравнения r(x)−s(x)=0 мы всегда можем преобразовать в тождественно равную рациональную дробь вида .
Так мы от исходного дробного рационального уравнения r(x)=s(x) переходим к уравнению , а его решение, как мы выяснили выше, сводится к решению уравнения p(x)=0 .
Но здесь обязательно надо учитывать тот факт, что при замене r(x)−s(x)=0 на , и дальше на p(x)=0 , может произойти расширение области допустимых значений переменной x .
Следовательно, исходное уравнение r(x)=s(x) и уравнение p(x)=0 , к которому мы пришли, могут оказаться неравносильными, и, решив уравнение p(x)=0 , мы можем получить корни, которые будут посторонними корнями исходного уравнения r(x)=s(x) . Выявить и не включать в ответ посторонние корни можно, либо выполнив проверку, либо проверив их принадлежность ОДЗ исходного уравнения.
Обобщим эту информацию в алгоритм решения дробного рационального уравнения r(x)=s(x) . Чтобы решить дробное рациональное уравнение r(x)=s(x) , надо
- Получить справа нуль с помощью переноса выражения из правой части с противоположным знаком.
- Выполнить действия с дробями и многочленами в левой части уравнения, тем самым преобразовав ее в рациональную дробь вида .
- Решить уравнение p(x)=0 .
- Выявить и исключить посторонние корни, что делается посредством их подстановки в исходное уравнение или посредством проверки их принадлежности ОДЗ исходного уравнения.
Для большей наглядности покажем всю цепочку решения дробных рациональных уравнений:
.
Давайте рассмотрим решения нескольких примеров с подробным пояснением хода решения, чтобы прояснить приведенный блок информации.
Пример.
Решите дробное рациональное уравнение .
Решение.
Будем действовать в соответствии с только что полученным алгоритмом решения. И сначала перенесем слагаемые из правой части уравнения в левую, в результате переходим к уравнению .
На втором шаге нам нужно преобразовать дробное рациональное выражение в левой части полученного уравнения к виду дроби . Для этого выполняем приведение рациональных дробей к общему знаменателю и упрощаем полученное выражение: . Так мы приходим к уравнению .
На следующем этапе нам нужно решить уравнение −2·x−1=0 . Находим x=−1/2 .
Остается проверить, не является ли найденное число −1/2 посторонним корнем исходного уравнения. Для этого можно сделать проверку или найти ОДЗ переменной x исходного уравнения. Продемонстрируем оба подхода.
Начнем с проверки. Подставляем в исходное уравнение вместо переменной x число −1/2 , получаем , что то же самое, −1=−1 . Подстановка дает верное числовое равенство, поэтому, x=−1/2 является корнем исходного уравнения.
Теперь покажем, как последний пункт алгоритма выполняется через ОДЗ. Областью допустимых значений исходного уравнения является множество всех чисел, кроме −1 и 0 (при x=−1 и x=0 обращаются в нуль знаменатели дробей). Найденный на предыдущем шаге корень x=−1/2 принадлежит ОДЗ, следовательно, x=−1/2 является корнем исходного уравнения.
Ответ:
−1/2 .
Рассмотрим еще пример.
Пример.
Найдите корни уравнения .
Решение.
Нам требуется решить дробно рациональное уравнение, пройдем все шаги алгоритма.
Во-первых, переносим слагаемое из правой части в левую, получаем .
Во-вторых, преобразуем выражение, образовавшееся в левой части: . В результате приходим к уравнению x=0 .
Его корень очевиден – это нуль.
На четвертом шаге остается выяснить, не является ли найденный корень посторонним для исходного дробно рационального уравнения. При его подстановке в исходное уравнение получается выражение . Очевидно, оно не имеет смысла, так как содержит деление на нуль. Откуда заключаем, что 0 является посторонним корнем. Следовательно, исходное уравнение не имеет корней.
7 , что приводит к уравнению . Отсюда можно заключить, что выражение в знаменателе левой части должно быть равно из правой части, то есть, . Теперь вычитаем из обеих частей тройки: . По аналогии , откуда , и дальше .
Проверка показывает, что оба найденных корня являются корнями исходного дробного рационального уравнения.
Ответ:
Список литературы.
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 16-е изд. - М. : Просвещение, 2008. - 271 с. : ил. - ISBN 978-5-09-019243-9.
- Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. - 11-е изд., стер. - М.: Мнемозина, 2009. - 215 с.: ил. ISBN 978-5-346-01155-2.
- Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 16-е изд. - М. : Просвещение, 2009. - 271 с. : ил. - ISBN 978-5-09-021134-5.











 Ответ: 0
Ответ: 0
 В.
В. Г.
Г.
 2)
2)
 3)
3)
 .
Какие из них не имеют смысл при у = 2?
.
Какие из них не имеют смысл при у = 2? имеет корни:
имеет корни: В.
В.


 имеет корни:
имеет корни: 2)
2)
 3)
3)
 Какие из них не имеют смысл при х = 0?
Какие из них не имеют смысл при х = 0? имеет корни:
имеет корни: Б.
Б.
 В.
В. имеет корни:
имеет корни: