Интегрирование простейших рациональных функций. Интегрирование дробно-рациональной функции

Рациональная функция - это дробь вида , числитель и знаменатель которой - многочлены или произведения многочленов.

Пример 1. Шаг 2.

.

Умножаем неопределённые коэффициенты на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях:

Раскрываем скобки и приравниваем полученое к полученному выражению числитель исходной подынтегральной дроби:

В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и составляем из них систему уравнений:

.

Сокращаем все иксы и получаем эквивалентную систему уравнений:

.

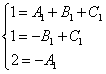Таким образом, окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 2. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

Теперь начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:

Теперь требуется составить и решить систему уравнений. Для этого приравниваем коэффициенты при переменной в соответствующей степени в числителе исходного выражения функции и аналогичные коэффициенты в полученном на предыдущем шаге выражения:

Решаем полученную систему:

Итак, , отсюда

.

Пример 3. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:

Как и в предыдущих примерах составляем систему уравнений:

Сокращаем иксы и получаем эквивалентную систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 4. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

Как приравнивать числитель исходной дроби к выражению в числителе, полученному после разложения дроби на сумму простых дробей и приведения этой суммы к общему знаменателю, мы уже знаем из предыдуших примеров. Поэтому лишь для контроля приведём получившуюся систему уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 5. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

Самостоятельно приводим к общему знаменателю эту сумму, приравнивать числитель этого выражения к числителю исходной дроби. В результате должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

.

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 6. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Производим с этой суммой те же действия, что и в предыдущих примерах. В результате должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

.

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 7. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

После известных действий с полученной суммой должна получиться следующая система уравнений:

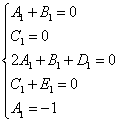
Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 8. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

Внесём некоторые изменения в уже доведённые до автоматизма действия для получения системы уравнений. Есть искусственный приём, который в некоторых случаях помогает избежать лишних вычислений. Приводя сумму дробей к общему знаменателю получаем и приравнивая числитель этого выражения к числителю исходной дроби, получаем.

Ранее речь шла об общих приемах интегрирования. В этом и следующих параграфах мы будем говорить об интегрировании конкретных классов функций с помощью рассмотренных приемов.

Интегрирование простейших рациональных функций

Рассмотрим интеграл вида \textstyle{\int R(x)\,dx} , где y=R(x) - рациональная функция. Всякое рациональное выражение R(x) можно представить в виде \frac{P(x)}{Q(x)} , где P(x) и Q(x) - многочлены. Если эта дробь неправильная, т. е. если степень числителя больше или равна степени знаменателя, то ее можно представить в виде суммы многочлена (целая часть) и правильной дроби. Поэтому достаточно рассмотреть интегрирование правильных дробей.

Покажем, что интегрирование таких дробей сводится к интегрированию простейших дробей , т. е. выражений вида:

\mathsf{1)}~\frac{A}{x-a};\quad \mathsf{2)}~\frac{A}{(x-a)^n};\quad \mathsf{3)}~ \frac{Ax+B}{x^2+px+q};\quad \mathsf{4)}~\frac{Ax+B}{(x^2+px+q)^n}.

где A,\,B,\,a,\,p,\,q - действительные числа, а квадратный трехчлен x^2+px+q не имеет действительных корней. Выражения вида 1) и 2) называют дробями 1-го рода, а выражения вида 3) и 4) - дробями 2-го рода.

Интегралы от дробей 1-го рода вычисляются непосредственно

\begin{aligned}\mathsf{1)}&~\int\frac{A}{x-a}\,dx= A\ln|x-a|+C;\\ \mathsf{2)}&~ \int\frac{A}{(x-a)^n}\,dx= A\int(x-a)^{-n}\,dx= A\,\frac{(x-a)^{-n+1}}{-n+1}+C~(n=2,3,4,\ldots). \end{aligned}

Рассмотрим вычисление интегралов от дробей 2-го рода: \mathsf{3)}~ \int\frac{Ax+B}{x^2+px+q}\,dx\,.

Сначала заметим, что

\int\frac{dt}{t^2+a^2}= \frac{1}{a}\operatorname{arctg}\frac{t}{a}+C,\qquad \int\frac{t\,dt}{t^2+a^2}= \frac{1}{2}\ln(t^2+a^2)+C.

Чтобы свести вычисление интеграла 3) к этим двум интегралам, преобразуем квадратный трехчлен x^2+px+q , выделив из него полный квадрат:

x^2+px+q= {\left(x+\frac{p}{2}\right)\!}^2+ \left(q-\frac{p^2}{4}\right)\!.

Так как по предположению этот трехчлен не имеет действительных корней, то q-\frac{p^2}{4}>0 и мы можем положить q-\frac{p^2}{4}=a^2 . Подстановка x+\frac{p}{2}=t,~ dx=dt преобразует интеграл 3) к линейной комбинации указанных двух интегралов:

\begin{aligned}\int\frac{Ax+B}{x^2+px+q}\,dx&= \int\frac{A\!\left(t-\frac{p}{2}\right)+B}{t^2+a^2}\,dt= A\int\frac{t\,dt}{t^2+a^2}+ \left(B-\frac{Ap}{2}\right)\!\int\frac{dt}{t^2+a^2}=\\ &=\frac{A}{2}\ln(t^2+a^2)+ \frac{1}{a}\!\left(B-\frac{Ap}{2}\right)\!\ \operatorname{arctg}\frac{t}{a}+C. \end{aligned}

В окончательном ответе нужно лишь заменить {t} на x+\frac{p}{2} , а {a} на \sqrt{q-\frac{p^2}{4}} . Так как t^2+a^2=x^2+px+q , то

\int\frac{Ax+B}{x^2+px+q}\,dx= \frac{A}{2}\ln(x^2+px+q)+ \frac{B-\dfrac{Ap}{2}}{\sqrt{q-\dfrac{p^2}{4}}} \operatorname{arctg}\frac{x+\dfrac{p}{2}}{\sqrt{q-\dfrac{p^2}{4}}}+C.

Рассмотрим случай \mathsf{4)}~ \int\frac{Ax+B}{(x^2+px+q)^n}\,dx .

Как и в предыдущем случае, положим x+\frac{p}{2}=t . Получим:

\int\frac{Ax+B}{(x^2+px+q)^n}\,dx= A\int\frac{t\,dt}{(t^2+a^2)^n}+ \left(B-\frac{Ap}{2}\right)\! \int\frac{dt}{(t^2+a^2)^n}\,.

Первое слагаемое вычисляется так:

A\int\frac{t\,dt}{(t^2+a^2)^n}= \frac{A}{2}\int(t^2+a^2)^{-n}\,d(t^2+a^2)= \frac{A}{2}\frac{(t^2+a^2)^{-n+1}}{-n+1}= \frac{A}{2(1-n)(t^2+a^2)^{n-1}}\,.

Второй же интеграл вычисляется с помощью рекуррентной формулы.

Пример 1. Вычислим \int\frac{3x+2}{x^2+2x+3}\,dx .

Решение. Имеем: x^2+2x+3=(x+1)^2+2 . Положим x+1=t . Тогда dx=dt и 3x+2=3(t-1)+2=3t-1 и, следовательно,

\begin{aligned}\int\frac{3x+2}{x^2+2x+3}\,dx&= \int\frac{3t-1}{t^2+2}\,dt= \frac{3}{2}\int\frac{2t\,dt}{t^2+2}- \int\frac{dt}{t^2+(\sqrt{2})^2}=\\ &=\frac{3}{2}\ln(t^2+2)- \frac{1}{\sqrt{2}}\operatorname{arctg}\frac{t}{\sqrt{2}}+C=\\ &=\frac{3}{2}\ln(x^2+2x+3)- \frac{1}{\sqrt{2}}\operatorname{arctg}\frac{x+1}{\sqrt{2}}+C. \end{aligned}

Пример 2. Вычислим \int\frac{x+2}{(x^2+6x+10)^2}\,dx .

Решение. Имеем: x^2+6x+10=(x+3)^2+1 . Введем новую переменную, положив x+3=t . Тогда dt=dx и x+2=t-1 . Заменив переменную под знаком интеграла, получим:

\begin{aligned}\int\frac{x+2}{(x^2+6x+10)^2}\,dx&= \int\frac{t-1}{(t^2+1)^2}\,dt= \frac{1}{2}\int\frac{2t\,dt}{(t^2+1)^2}-\int\frac{dt}{(t^2+1)^2}=\\ &=-\frac{1}{2(t^2+1)}- \int\frac{dt}{(t^2+1)^2}\,. \end{aligned}}

Положим I_2=\int\frac{dt}{(t^2+1)^2} . Имеем:

I_2=\frac{1}{2}I_1+\frac{1}{2}\frac{t}{t^2+1} , но I_1=\int\frac{dt}{t^2+1}= \operatorname{arctg}t Таким образом, I_2= \frac{1}{2}\operatorname{arctg}t+ \frac{t}{2(t^2+1)} .

Окончательно получаем:

\begin{aligned}\int\frac{x+2}{(x^2+6x+10)^2}\,dx&=-\frac{1}{2(t^2+1)}-\frac{1}{2}\operatorname{arctg}t-\frac{t}{2(t^2+1)}=\\ &=-\frac{1}{2(x^2+6x+10)}- \frac{1}{2}\operatorname{arctg}(x+3)- \frac{x+3}{2(x^2+6x+10)}+C=\\ &=\frac{-x-4}{2(x^2+6x+10)}-\frac{1}{2}\operatorname{arctg}(x+3)+C \end{aligned}

Интегрирование правильных дробей

Рассмотрим правильную дробь R(x)=\frac{P(x)}{Q(x)} , где Q(x) - многочлен степени n . Не теряя общности, можно считать, что старший коэффициент в Q(x) равен 1. В курсе алгебры доказывается, что такой многочлен с действительными коэффициентами может быть разложен на множители первой и второй степени с действительными коэффициентами:

Q(x)= (x-x_1)^{\alpha}\ldots (x-x_k)^{\beta} (x^2+p\,x+q)^{\gamma}\ldots (x^2+r\,x+s)^{\delta}.

где x_1,\ldots,x_k -действительные корни многочлена Q(x) , а квадратные трехчлены не имеют действительных корней. Можно доказать, что тогда R(x) представляется в виде суммы простейших дробей вида 1) -4):

\begin{aligned}R(x)=&\frac{P(x)}{Q(x)}= \frac{A_1}{(x-x_1)^{\alpha}}+ \frac{A_2}{(x-x_1)^{\alpha-1}}+\ldots+ \frac{A_{\alpha}}{x-x_1}\,+\\ &+\,\ldots+ \frac{B_1}{(x- x_k)^{\beta}}+ \frac{B_2}{(x-x_k)^{\beta-1}}+\ldots+ \frac{B_{\beta}}{x-x_k}+ \frac{M_1x+ N_1}{(x^2+p\,x+q)^{\gamma}}\,+\\ &+\,\ldots+ \frac{M_{\gamma}+ N_{\gamma}}{x^2+ p\,x+s}+ \frac{E_1x+F_1}{(x^2+rx+s)^{\delta}}+\ldots+ \frac{E_{\delta}x+F_{\delta}}{x^2+rx+s}\, \end{aligned}

где показатели у знаменателей последовательно уменьшаются от \alpha до 1, …, от \beta до 1, от \gamma до 1, …, от \delta до 1, а A_1,\ldots,F_{\delta} - неопределенные коэффициенты. Для того чтобы найти эти коэффициенты, необходимо освободиться от знаменателей и, получив равенство двух многочленов, воспользоваться методом неопределенных коэффициентов.

Другой способ определения коэффициентов A_1,\ldots, A_{\alpha}, \ldots, F_{\delta} основан на подстановке значений переменной x . Подставляя в равенство, полученное из равенства (1) после освобождения от знаменателей, вместо x любое число, придем к линейному уравнению относительно искомых коэффициентов. Путем подстановки необходимого количества таких частных значений переменной получим систему уравнений для отыскания коэффициентов. В качестве частных значений переменной удобнее всего выбирать корни знаменателя (как действительные, так и комплексные). При этом почти все члены в правой части равенства (имеется в виду равенство двух многочленов) обращаются в нуль, что позволяет легко находить оставшиеся коэффициенты. При подстановке комплексных значений следует иметь в виду, что два комплексных числа равны тогда и только тогда, когда равны соответственно их действительные и мнимые части. Поэтому из каждого равенства, содержащего комплексные числа, получаются два уравнения.

После нахождения неопределенных коэффициентов остается вычислить интегралы от полученных простейших дробей. Так как при интегрировании простейших дробей получаются, как мы видели, лишь рациональные функции, арктангенсы и логарифмы, то интеграл от любой рациональной функции выражается через рациональную функцию, арктангенсы и логарифмы .

Пример 3. Вычислим интеграл от правильной рациональной дроби \int\frac{6x+1}{x^2+2x-3}\,dx .

Решение. Разложим знаменатель подынтегральной функции на множители:

x^2+2x-3=(x-1)(x+3).

Выпишем подынтегральную функцию и представим ее в виде суммы простейших дробей:

\frac{6x+1}{x^2+2x-3}= \frac{A}{x-1}+\frac{B}{B+3}\,.

6x+1=A\cdot (x+3)+B\cdot (x-1)\,.

Для отыскания коэффициентов воспользуемся методом подстановки частных значений. Для нахождения коэффициента A положим x=1 . Тогда из равенства (2) получим 7=4A , откуда A=7/4 . Для отыскания коэффициента B положим x=-3 . Тогда из равенства (2) получим -17=-4B , откуда B=17/4 .

Итак, \frac{6x+1}{x^2+2x-3}= \frac{7}{4}\cdot\frac{1}{x-1}+ \frac{17}{4}\cdot\frac{1}{x+3} . Значит,

\int\frac{6x+1}{x^2+2x-3}\,dx= \frac{7}{4}\int\frac{dx}{x-1}+ \frac{17}{4}\int\frac{dx}{x+3}= \frac{7}{4}\ln|x-1|+ \frac{17}{4}\ln|x+3|+C.

Пример 4. Вычислим \int\frac{x^4+2x^2+8x+5}{(x^2+2)(x-1)^2(x+2)}\,dx .

Решение. Выпишем подынтегральную функцию и представим ее в виде суммы простейших дробей. В знаменателе содержится множитель x^2+2 , не имеющий действительных корней, ему соответствует дробь 2-го рода: \frac{Ax+B}{x^2+2} множителю (x-1)^2 соответствует сумма двух дробей 1-го рода: \frac{C}{(x-1)^2}+ \frac{D}{x-1} ; наконец, множителю x+2 соответствует одна дробь 1-го рода \frac{E}{x+2} . Таким образом, подынтегральную функцию мы представим в виде суммы четырех дробей:

\frac{x^4+2x^2+8x+5}{(x^2+2)(x-1)^2(x+2)}= \frac{Ax+B}{x^2+2}+ \frac{C}{(x-1)^2}+ \frac{D}{x-1}+ \frac{E}{x+2}\,.

\begin{aligned} x^4+2x^2+8x+5&= (Ax+B)(x-1)^2(x+2)+ C(x^2+2)(x+2)\,+\\ &\phantom{=}+ D(x^2+2)(x-1)(x+2)+ E(x^2+2)(x-1)^2.\end{aligned}

Знаменатель подынтегральной функции имеет два действительных корня: x=1 и x=-2 . При подстановке в равенство (4) значения x=1 получаем 16=9C , откуда находим C=16/9 . При подстановке x=-2 получаем 13=54E и соответственно определяем E=13/54 . Подстановка значения x=i\,\sqrt{2} (корня многочлена x^2+2 ) позволяет перейти к равенству

4-4+8\,i\,\sqrt{2}+5= (A\,i\,\sqrt{2}+B)\cdot (i\,\sqrt{2}-1)^2\cdot (i\,\sqrt{2}+2).

Оно преобразуется к виду:

(10A+2B)+(2A-5B)\sqrt{2}\,i= 5+8\sqrt{2}\,i , откуда 10A+2B=5 , а (2A-5B)\sqrt{2}=8\sqrt{2} .

Решив систему двух уравнений с двумя переменными \begin{cases}10A+2B=5,\\ 2A-5B=8,\end{cases} находим: A=\frac{41}{54},~ B=-\frac{35}{27} .

Осталось определить значение коэффициента D . Для этого в равенстве (4) раскроем скобки, приведем подобные члены, а затем сравним коэффициенты при x^4 . Получим:

A+D+E=1 , то есть D=0 .

Подставим найденные значения коэффициентов в равенство (3):

\frac{x^4+2x^2+8x+5}{(x^2+2)(x-1)^2(x+2)}= \frac{\drac{41}{54}\,x- \dfrac{35}{27}}{x^2+2}+ \frac{16}{9}\frac{1}{(x-1)^2}+ \frac{13}{54}\frac{1}{x+2}\,

\begin{aligned}\int\frac{x^4+2x^2+8x+5}{(x^2+2)(x-1)^2(x+2)}\,dx&= \frac{41}{54}\int\frac{x\,dx}{x^2+2}- \frac{35}{27}\int\frac{dx}{x^2+2}+ \frac{16}{9} \int\frac{dx}{(x-1)^2}+ \frac{13}{54}\int\frac{dx}{x+2}=\\ &=\frac{41}{108}\ln(x^2+2)- \frac{35}{27\sqrt{2}}\operatorname{arctg}\frac{x}{\sqrt{2}}- \frac{16}{9(x-1)}+ \frac{13}{54} \ln|x+2|+C.\end{aligned}

Интегрирование неправильных дробей

Пусть нужно проинтегрировать функцию y=\frac{f(x)}{g(x)} , где f(x) и g(x) - многочлены, причем степень многочлена f(x) больше или равна степени многочлена g(x) . В этом случае прежде всего необходимо выделить целую часть неправильной дроби \frac{f(x)}{g(x)} , т. е. представить ее в виде

\frac{f(x)}{g(x)}=s(x)+ \frac{r(x)}{g(x)}\,

где s(x) - многочлен степени, равной разности степеней многочленов f(x) и g(x) , а \frac{r(x)}{g(x)} - правильная дробь.

Тогда имеем \int\frac{f(x)}{g(x)}\,dx= \int s(x)\,dx+ \int\frac{r(x)}{g(x)}\,dx\,. .

Пример 5. Вычислим интеграл от неправильной дроби \int\frac{x^4-4x^3+x^2+16x-11}{(x-1)(x+2)(x-3)}\,dx .

Решение. Имеем:

\begin{aligned}g(x)&=(x-1)(x+2)(x-3)= x^3-2x^2-5x+6,\\ f(x)&=x^4-4x^3+x^2+16x-11. \end{aligned}

Для выделения целой части разделим f(x) на g(x) : \frac{f(x)}{g(x)}= x-2+\frac{2x^2+1}{x^3-2x^2-5x+6}\,.

Значит, \int\frac{x^4-4x^3+x^2+16x-11}{(x-1)(x+2)(x-3)}\,dx= \int(x-2)dx+ \int\frac{2x^2+1}{(x-1)(x+2)(x-3)}\,dx

Имеем: \int(x-2)dx=\frac{x^2}{2}-2x+C .

Для вычисления интеграла \int\frac{2x^2+1}{(x-1)(x+2)(x-3)}\,dx применяется, как и выше, метод неопределенных коэффициентов. После вычислений, которые мы оставляем читателю, получаем.

Здесь мы приводим подробные решения трех примеров интегрирования следующих рациональных дробей:
, , .

Пример 1

Вычислить интеграл:
.

Решение

Здесь под знаком интеграла стоит рациональная функция, поскольку подынтегральное выражение является дробью из многочленов. Степень многочлена знаменателя (3 ) меньше степени многочлена числителя (4 ). Поэтому, вначале необходимо выделить целую часть дроби.

1. Выделим целую часть дроби. Делим x 4 на x 3 - 6 x 2 + 11 x - 6 :

Отсюда
.

2. Разложим знаменатель дроби на множители. Для этого нужно решить кубическое уравнение:
.
6
1, 2, 3, 6, -1, -2, -3, -6 .
Подставим x = 1 :
.

1 . Делим на x - 1 :

Отсюда
.
Решаем квадратное уравнение .
.
Корни уравнения: , .
Тогда
.

3. Разложим дробь на простейшие.

.

Итак, мы нашли:
.
Интегрируем.

Ответ

Пример 2

Вычислить интеграл:
.

Решение

Здесь в числителе дроби - многочлен нулевой степени (1 = x 0 ). В знаменателе - многочлен третьей степени. Поскольку 0 < 3 , то дробь правильная. Разложим ее на простейшие дроби.

1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение третьей степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 3 (члена без x ). То есть целый корень может быть одним из чисел:
1, 3, -1, -3 .
Подставим x = 1 :
.

Итак, мы нашли один корень x = 1 . Делим x 3 + 2 x - 3 на x - 1 :

Итак,
.

Решаем квадратное уравнение:
x 2 + x + 3 = 0 .
Находим дискриминант: D = 1 2 - 4·3 = -11 . Поскольку D < 0 , то уравнение не имеет действительных корней. Таким образом, мы получили разложение знаменателя на множители:
.

2.
.
(x - 1)(x 2 + x + 3) :
(2.1) .
Подставим x = 1 . Тогда x - 1 = 0 ,
.

Подставим в (2.1) x = 0 :
1 = 3 A - C ;
.

Приравняем в (2.1) коэффициенты при x 2 :
;
0 = A + B ;
.

.

3. Интегрируем.
(2.2) .
Для вычисления второго интеграла, выделим в числителе производную знаменателя и приведем знаменатель к сумме квадратов.

;
;
.

Вычисляем I 2 .


.
Поскольку уравнение x 2 + x + 3 = 0 не имеет действительных корней, то x 2 + x + 3 > 0 . Поэтому знак модуля можно опустить.

Поставляем в (2.2) :
.

Ответ

Пример 3

Вычислить интеграл:
.

Решение

Здесь под знаком интеграла стоит дробь из многочленов. Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3 . Степень многочлена знаменателя дроби равна 4 . Поскольку 3 < 4 , то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.

1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение четвертой степени:
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x ). То есть целый корень может быть одним из чисел:
1, 2, -1, -2 .
Подставим x = -1 :
.

Итак, мы нашли один корень x = -1 . Делим на x - (-1) = x + 1 :


Итак,
.

Теперь нужно решить уравнение третьей степени:
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x ). То есть целый корень может быть одним из чисел:
1, 2, -1, -2 .
Подставим x = -1 :
.

Итак, мы нашли еще один корень x = -1 . Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.

Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то мы получили разложение знаменателя на множители:
.

2. Разложим дробь на простейшие. Ищем разложение в виде:
.
Освобождаемся от знаменателя дроби, умножаем на (x + 1) 2 (x 2 + 2) :
(3.1) .
Подставим x = -1 . Тогда x + 1 = 0 ,
.

Продифференцируем (3.1) :

;

.
Подставим x = -1 и учтем, что x + 1 = 0 :
;
; .

Подставим в (3.1) x = 0 :
0 = 2 A + 2 B + D ;
.

Приравняем в (3.1) коэффициенты при x 3 :
;
1 = B + C ;
.

Итак, мы нашли разложение на простейшие дроби:
.

3. Интегрируем.


.

Контрольную работу на интегрирование функций, в том числе и рациональных дробей задают студентам 1, 2 курсов. Примеры интегралов в основном будут интересны для математиков, экономистов, статистов. Данные примеры задавали на контрольной работе в ЛНУ им. И. Франка. Условия следующих примеров "Найти интеграл" или "Вычислить интеграл", поэтому для экономии места и Вашего времени их не выписывали.

Пример 15. Мы пришли к интегрированию дробно-рациональных функций . Они занимают особое место среди интегралов, поскольку требуют много времени на вычисление и помогают преподавателям проверить Ваши знания не только по интегрированию. Для упрощения функции под интегралом добавим и вычтем в числителе выражение, которое позволит разбить функцию под интегралом на две простые

В результате один интеграл находим довольно быстро, во втором нужно дробь разложить на суму элементарных дробей

При сведении к общему знаменателю получим такие числительные

Далее раскрываем скобки и группируем

Приравниваем значение при одинаковых степенях "икс" справа и слева. В результате придем к системе трех линейных уравнений (СЛАУ) с тремя неизвестными.

Как решать системы уравнений описано в других статьях сайта. В конечном варианте Вы получите следующее решения СЛАУ
A=4; B=-9/2; C=-7/2.
Подставляем постоянные в разложение дроби на простейшие и выполняем интегрирование


На этом пример решен.

Пример 16. Опять нужно найти интеграл от дробно-рациональной функции. Для начала кубическое уравнение, которое содержится в знаменателе дроби разложим на простые множители

Далее выполняем разложение дроби на простейшие

Сводим правую сторону к общему знаменателю и раскрываем скобки в числителе.


Приравниваем коэффициенты при одинаковых степенях переменной. Снова придем к СЛАУ с тремя неизвестными

Подставляем значения А,В,С в разложение и вычисляем интеграл

Первые два слагаемых дают логарифм, последний тоже легко найти.

Пример 17. В знаменателе дробно-рациональной функции имеем разницу кубов. Ее по формулам сокращенного умножения раскладываем на два простых множителя

Далее полученную дробную функцию расписываем на сумму простых дробей и сводим их под общий знаменатель

В числителе получим следующее выражение.

Из него формируем систему линейных уравнений для вычисления 3 неизвестных

A=1/3; B=-1/3; C=1/3.
Подставляем А, В, С в формулу и выполняем интегрирование. В результате придем к такому ответу


Здесь числитель второго интеграла превращали в логарифм, при этом остаток под интегралом дает арктангенс.
Подобных примеров на интегрирование рациональных дробей в интернете очень много. Похожие примеры Вы можете найти из приведенных ниже материалов.