Цели урока:

• Ввести понятие параллельных плоскостей.
• Рассмотреть и доказать теоремы, выражающие признак параллельности плоскостей и свойства параллельных плоскостей.
• Проследить применение этих теорем при решении задач.

План урока (записать на доске):

I. Подготовительная устная работа.

II. Изучение нового материала:

1. Взаимное расположение двух плоскостей в пространстве.
2. Определение параллельных плоскостей.
3. Признак параллельности плоскостей.
4. Свойство параллельных плоскостей.

III. Итог урока.

IV. Домашнее задание.

ХОД УРОКА

I. Устная работа

Начать урок хочется с цитаты из философского письма Чаадаева:

“Откуда это чудодейственная мощь анализа в математике? Дело в том, что ум здесь действует в полном подчинении данному правилу”.

Это подчинение правилу мы рассмотрим на следующем задании. Для усвоения нового материала необходимо повторить некоторые вопросы. Для этого надо установить утверждение, которое следует из данных утверждений и обосновать свой ответ:

II. Изучение нового материала

1. Как могут располагаться две плоскости в пространстве? Что представляет собой множество точек, принадлежащих обеим плоскостям?

Ответ:

а) совпадать (тогда дело будем иметь с одной плоскостью, не устраивает);
б) пересекаться, ;
в) не пересекаться (общих точек вообще нет).

2. Определение: Если две плоскости не пересекаются, то они называются параллельными

3. Обозначение:

4. Приведите примеры параллельных плоскостей из окружающей обстановки

5. Как выяснить параллельны ли какие-либо две плоскости в пространстве?

Ответ:

Можно воспользоваться определением, но это нецелесообразно, т.к. установить пересечение плоскостей не всегда возможно. Поэтому необходимо рассмотреть условие достаточное для того, чтобы утверждать о параллельности плоскостей.

6. Рассмотрим ситуации:

б) если ?

в) если ?

Почему в а) и б) ответ: "не всегда", а в в) "да"? (Пересекающиеся прямые определяют плоскость единственным образом, значит определены однозначно!)

Ситуация 3 и есть признак параллельности двух плоскостей.

7. Теорема: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Дано:

Доказать:

Доказательство:

(Обозначения на чертеж наносят учащиеся).

1. Отметим: . Аналогично:
2. Пусть: .
3. Имеем: Аналогично:
4. Получим: через М проходит противоречие с аксиомой планиметрии.
5. Итак: неверно, значит , ч. и т. д.

8. Решить № 51 (Обозначения на чертеж наносят учащиеся).

Дано:

Доказать:

Доказательство:

1 способ

1. Построим

2 способ

Ввести через через .

9. Рассмотрим два свойства параллельных плоскостей:

Теорема: Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

(Достраивают и наносят обозначение на чертеж сами учащиеся).

Дано:

( I курс)

Преподаватель математики ПУ№3

Туаева З.С.

2015г.

Тема урока “Параллельность плоскостей”

Тип урока: урок усвоения нового материала.

Основная цель:

Ввести понятие параллельных плоскостей.

Доказать признак параллельности двух плоскостей.

Рассмотреть свойства параллельных плоскостей.

Задачи:

Обучающие :

Сформировать навык применения признака параллельности двух плоскостей и изученных свойств параллельных плоскостей при решении задач.

Развивающие :

Развитие пространственного воображения обучающихся,

Развитие мыслительной деятельности обучающихся.

Развитие логичного, рационального, критичного, творческого мышления и познавательных способностей обучающихся.

Воспитательные :

Воспитание аккуратности, графической грамотности.

Использование новых образовательных технологий: использование технологии проблемного обучения.

План урока

Определение параллельных плоскостей.

Признак параллельности двух плоскостей.

Свойства параллельных плоскостей.

Беседа с учащимися по вопросам, при которой преподаватель, систематически создавая проблемные ситуации и организуя деятельность учащихся по решению учебных проблем, обеспечивает оптимальное сочетание их самостоятельной, поисковой деятельности с усвоением готовых выводов науки.

III . Формирование умений и навыков

Решение учащимися задач на применение признака параллельности двух плоскостей и свойств параллельных плоскостей . Самостоятельная работа для контроля усвоенного и проведения первичного закрепления материала

IV . Домашнее задание

Комментарии учителя по домашнему заданию

Ход урока:

1. Сообщение темы и цели урока. Сообщение плана урока.

2. Этап актуализации знаний.

Вопросы к учащимся:

1. Какие прямые в пространстве называются параллельными?

(Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек)

2. Сформулируйте определение параллельности прямой и плоскости?

(Прямая и плоскость называются параллельными, если они не имеют общих точек)

3. Сформулируйте третью аксиому стереометрии?

(Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей)

4. Как могут располагаться две плоскости в пространстве?

(Две плоскости либо пересекаются по прямой (рис.1, а), либо не пересекаются (рис.1, б))

Рис.1, а Рис.1, б

3. Изучение нового материала.

1. Учебная проблема : дать определение параллельных плоскостей.

Учебная ситуация :

Вопросы к учащимся:

1. Сколько общих точек имеют две непересекающиеся плоскости?

(Ни одной общей точки)

2. Как называются плоскости, которые не имеют ни одной общей точки?

(Параллельные плоскости)

3. Сформулируйте определение параллельных плоскостей, учитывая количество их общих точек?

Две плоскости называются параллельными, если они не имеют общих точек.

4. Укажите модели параллельных плоскостей на предметах классной обстановки?

(Пол и потолок кабинета, две противоположные стены, поверхность стола и плоскость пола)

2. Учебная проблема : сформулировать и доказать признак параллельности двух плоскостей.

Учебная ситуация :

Учащимся предоставляется модель параллелепипеда.

Вопросы к учащимся:

1. Какого взаимное расположение плоскостей и ?

(плоскости и параллельны)

2. Назовите любые две пересекающиеся прямые плоскости

(прямая АВ, прямая ВС)

3. Назовите прямые плоскости , параллельные прямым АВ и ВС ?

(
║
║

4. Какого взаимное расположение прямой АВ и плоскости ? Ответ обоснуйте.

(АВ║ по признаку параллельности прямой и плоскости: если прямая, не лежащая в данной плоскости (
), параллельна какой-нибудь прямой, лежащей в этой плоскости (
║

Если учащиеся затрудняются обосновать ответ, то обратить их внимание на признак параллельности прямой и плоскости.

5. Какого взаимное расположение прямой ВС и плоскости ? Ответ обоснуйте.

(ВС║ по признаку параллельности прямой и плоскости: если прямая, не лежащая в данной плоскости(
), параллельна какой-нибудь прямой, лежащей в этой плоскости(
║
), то она параллельна самой плоскости)

6. Предположите, что плоскости и не параллельны. Как тогда они будут располагаться?

(плоскости будут пересекаться по некоторой прямой с)

7. Как в этом случае будут располагаться прямые АВ и с ?

(с ║АВ, согласно свойству
), параллельную другой плоскости (АВ║
║АВ))

8. Как в этом случае будут располагаться прямые ВС и с ?

(с ║ВС, согласно свойству : если плоскость проходит через данную прямую (
), параллельную другой плоскости (ВС║ ), и пересекает эту плоскость (
), то линия пресечения плоскостей параллельна данной прямой (с ║ВС))

9. Сколько прямых, параллельных прямой с , проходит через точку В ?

(Две прямые: прямая АВ, прямая ВС)

10. Возможно ли это?

(Это не возможно, так как по теореме о параллельных прямых: через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна)

11. Какой вывод можно сделать? Верно ли наше предположение?

(Наше предположение не верно, остается признать, что ║)

12. Сколько прямых необходимо в плоскости , чтобы плоскости и были параллельны?

(две прямые)

13. Какие между собой должны быть эти прямые?

(пересекающиеся)

14. Скольким прямым они должны быть параллельны из плоскости ?

(Двум)

15. Сформулируйте признак параллельности двух плоскостей, учитывая количество прямых одной плоскости, параллельных прямым другой плоскости?

Результат умозаключения обучающихся:

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

3. Учебная проблема : сформулировать и доказать свойства параллельных плоскостей.

Учебная ситуация :

Вопросы к учащимся:

и ?

(плоскости параллельны)

по отношению к плоскостям и ?

(плоскость пересекает плоскости и )

3. Что вы можете сказать про линии пересечения плоскостей?

(линии пересечения плоскостей параллельны между собой)

4. Ответ обоснуйте, используя определение параллельных прямых в пространстве.

(прямые а и в лежат в одной плоскости и не пересекаются, так как, если бы прямые пересекались, то плоскости и имели бы общую точку, что невозможно, так как эти плоскости параллельны)

5. Сформулируйте первое свойство параллельных плоскостей, учитывая взаимное расположение линий пересечений а и в ?

Результат умозаключения обучающихся:

Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

Учебная ситуация :

Учащимся предоставляется модель параллельных плоскостей, пересеченных третьей плоскостью.

Вопросы к учащимся:

1. Какого взаимное расположение плоскостей и ?

(плоскости параллельны)

2. Как располагается плоскость по отношению к плоскостям и ?

(плоскость пересекает плоскости и )

3. Что вы можете сказать про отрезки АВ и С D ?

(отрезки АВ и С D параллельны между собой)

4. Что вы можете сказать про отрезки АС и В D ?

(отрезки АС и В D параллельны между собой по свойству 1)

5. Как называется четырехугольник, у которого противоположные стороны попарно параллельны?

(параллелограмм)

6. Какие свойства параллелограмма вы знаете?

в параллелограмме противоположные стороны и углы равны

Диагонали параллелограмма точкой пресечения делятся пополам

7. Что вы можете сказать про отрезки АВ и С D , используя первое свойство параллелограмма?

(отрезки АВ и С D равны между собой)

8. Сформулируйте второе свойство параллельных плоскостей, используя равенство отрезков АВ и С D ?

Результат умозаключения обучающихся:

Отрезки параллельных прямых, заключенных между параллельными плоскостями равны.

4. Формирование умений и навыков.

Решение задач

Задача № 1. (№ 54) (На отработку признака параллельности двух плоскостей)

Дано :

Доказать :

║

Найти :

Доказательство:

1.
- средняя линия
MN ║ AC .

2. NP – средняя линия
NP ║ CD .

MN ║ AC
( MNP )║( ADC ) по признаку параллельности 2 пл.

NP ║ CD

4.
подобен
по третьему признаку подобия треугольников (если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны)
(так как отношение площадей двух подобных треугольников равно квадрату коэффициента подобия)

Ответ :
.

Задача № 2. (№ 63(а)) (На отработку 1 свойства параллельных плоскостей)

Дано:

║

Найти:

Решение:

1. Докажем, что
║
.

Так как

║(по условию)

║
.(по 1 свойству параллельных плоскостей)

2. Докажем, что
подобен
.

, как соответственные при
║
.и секущей

, как соответственные при
║
.и секущей

Значит,
подобен
по 2 углам.

3. Найдем
.

По условию

4. Найдем
.

Составим пропорцию :

Ответ :

Задача № 3. (№ 65) (На отработку 2 свойства параллельных плоскостей)

Дано :

║

║
║

Определить :

вид четырехугольников

Доказать:

Решение:

1. Рассмотрим четырехугольник
.

║
(по условию)

=

четырехугольник

2. Рассмотрим четырехугольник
.

║
(по условию)

=
(как отрезки параллельных прямых, заключенных между параллельными плоскостями, свойство 2)
четырехугольник
является параллелограммом (по 1 признаку параллелограмма: если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм)

3. Рассмотрим четырехугольник
.

║
(по условию)

=
(как отрезки параллельных прямых, заключенных между параллельными плоскостями, свойство 2)
четырехугольник
отсекает от треугольника треугольник, подобный данному. : ║ Домашнее задание.

§ 10 (п. 10-11) стр. (20-21)

№ 53, № 63(б).

Учебник: Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Л. С. Киселева, Э. Г. Позняк. Геометрия 10, 11. Москва “ Просвещение ” , 2002.

6. Итог урока.

Сегодня на уроке мы ввели понятие параллельных плоскостей, самостоятельно доказали признак параллельности двух плоскостей, рассмотрели свойства параллельных плоскостей. Научились решать задачи на доказательство с применением признака параллельности двух плоскостей, применять изученные свойства параллельных плоскостей при решении задач.

Параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Доказательство. Пусть a и b - данные плоскости, а 1 и а 2 – прямые в плоскости a , пересекающиеся в точке А , b 1 и b 2 соответственно параллельные им прямые в плоскости b . Допустим, что плоскости a и b не параллельны, то есть они пересекаются по некоторой прямой с . Прямая а 1 параллельна прямой b 1 , значит она параллельна и самой плоскости b (признак параллельности прямой и плоскости). Прямая а 2 параллельна прямой b 2 , значит она параллельна и самой плоскости b (признак параллельности прямой и плоскости). Прямая с принадлежит плоскости a , значит хотя бы одна из прямых а 1 или а 2 пересекает прямую с, то есть имеет с ней общую точку. Но прямая с также принадлежит и плоскости b , значит, пересекая прямую с, прямая а 1 или а 2 пересекает плоскость b , чего быть не может, так как прямые а 1 и а 2 параллельны плоскости b . Из этого следует, что плоскости a и b не пересекаются, то есть они параллельны.

Теорема 1 . Если две параллельные плоскости пересекаются третей, то прямые пересечения параллельны.
Доказательство. Пусть a и b - параллельные плоскости, а g - плоскость, пересекающая их. Плоскость a пересеклась с плоскостью g по прямой а. Плоскость b пересеклась с плоскостью g по прямой b . Линии пересечения а и b лежатв одной плоскости g и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.

Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.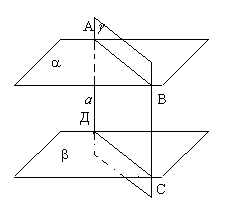
Доказательство. Пусть a и b - параллельные плоскости, а а и b – параллельные прямые, пересекающие их. Через прямые а и b проведем плоскость g (эти прямые параллельны, значит определяют плоскость, причем только одну). Плоскость a пересеклась с плоскостью g по прямой АВ. Плоскость b пересеклась с плоскостью g по прямой СД.По предыдущей теореме прямая с параллельна прямой d . Прямые а, b , АВ и СД принадлежат плоскости g .Четырехугольник, ограниченный этими прямыми,есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть АД = ВС

е свойство параллельных прямых, называемое транзитив ностью параллельности:

• Если две прямые а и b параллельны третьей прямой с, то они параллель ны друг другу.

Но доказать это свойство в стереометрии сложнее. На плоскости непараллельные прямые обязаны пересекаться и потому не могут быть одновременно параллельны третьей (иначе нарушается аксиома параллельных). В про странстве существуют непараллельные и при том непересекающиеся прямые если они лежат в разных плоскостях. О таких прямых говорят, что они скрещиваются.

На рис. 4 изображён куб; прямые АВ и ВС пересекаются, АВ и CD параллельны, а АВ и В С скрещиваются. В дальнейшем мы часто будем прибегать к помощи куба, чтобы иллюс трировать понятия и факты стереометрии. Наш куб склеен из шести граней-квадратов. Исходя из этого, мы будем выводить и другие его свойства. Например, можно утверждать, что прямая АВ параллельна C D, потому что обе они параллельны общей стороне CD со держащих их квадратов.

В стереометрии отношение параллельности рассматривается и для плоскостей: две пло скости или прямая и плоскость параллельны, если они не имеют общих точек. Прямую и плоскость удобно считать параллельными и в том случае, когда лежит в плоскости. Для плоскостей и прямых справедливы теоремы о транзитивности:

• Если две плоскости параллельны третьей плоскости, то они параллельны между собой.
• Если прямая и плоскость параллельны некоторой прямой(или плоскости), то они параллельны друг другу.

Наиболее важный частный случай второй теоремы- признак параллельности прямой и плоскости:

• Прямая параллельна плоскости, если она параллельна некоторой прямой в этой плоскости.

А вот признак параллельности плоскостей:

• Если две пересекающиеся прямые в одной плоскости соответственно параллельны двум пересекающимся прямым в другой плоскости, то и плоскости параллельны.

Часто используется и такая простая теорема:

• Прямые, по которым две параллельные плоскости пересекаются третьей, параллельны друг другу.

Посмотрим еще раз на куб (рис. 4). Из признака параллельности прямой и плоскости следует, например, что прямая А В параллельна плоскости АВСD (так как она параллельна прямой АВ в этой плоскости), а противоположные грани куба, в частности А В С D и ABCD, параллельны по признаку параллельности плоскостей: прямые A B и B С в одной грани соответственно параллельны прямым АВ и ВС в другой. И чуть менее простой пример. Плоскость, содержащая параллельные прямые AA и СС , пересекают параллельные плоскости АВСD и A B C D по прямым АС и А С , значит, эти прямые параллельны: аналогично, параллельные прямые В С и А D. Следовательно, параллельные плоскости АВ С и А DC, пересекающие куб по треугольникам.

III. Изображение пространственных фигур.

Есть такой афоризм Геометрия это искус ство правильно рассуждать на неправильном чертеже. Действительно, если вернуться к из ложенным выше рассуждениям, то окажется:

единственная польза, которую мы извлекли из сопровождавшего их рисунка куба, состоит в том, что он сэкономил нам место на объясне нии обозначений. С тем же успехом можно было изобразить его, как тело на рис. 4, я, хотя, очевидно, представленное на нём нечто не только не куб, но и не многогранник. И всё же в приведённом афоризме заключена лишь часть правды. Ведь прежде, чем рассуждать излагать готовое доказательство, надо его при думать. А для этого нужно ясно представлять себе заданную фигуру, соотношения между её элементами. Выработать такое представление помогает хороший чертёж. Более того, как мы увидим, в стереометрии удачный чертёж мо жет стать не просто иллюстрацией, а основой решения задачи.

Художник (вернее, художник-реалист) на рисует наш куб таким, каким мы его видим (рис. 5, б), т. е. в перспективе, или централь ной проекции. При центральной проекции из точки О (центр проекции) на плоскость а про извольная точка Х изображается точкой X, в которой а пересекается с прямой ОХ (рис. 6). Центральная проекция сохраняет прямоли нейное расположение точек, но, как правило, переводит параллельные прямые в пересека ющиеся, не говоря уже о том, что изменяет расстояния и углы. Изучение её свойств при вело к появлению важного раздела геометрии (см. статью Проективная геометрия).

Но в геометри-ческих чертежах исполь-зуется другая проекция. Можно сказать, что она получается из централь-ной когда центр О уда-ляется в бесконечность и прямые ОХ становятся па раллельными.

Выберем плоскость а и пересекающую её прямую l. Проведём через точку Х прямую, па раллельную l. Точка X, в которой эта прямая встречается с а, и есть параллельная проекция Х на плоскость, а вдоль прямой l (рис. 7). Про екция фигуры состоит из проекций всех её точек. В геометрии под изображением фигуры понимают её параллельную проекцию.

В частности, изображение прямой линии это прямая линия или (в исключительном слу чае, когда прямая параллельна направлению проекции) точка. На изображении параллель