Интегралы с бесконечными границами интегрирования. Несобственные интегралы от неограниченных функций

Называется Несобственным интегралом От функции F (X ) с бесконечным верхним пределом. Если этот предел существует и конечен, то несобственный интеграл называется Сходящимся . А если же он не существует или равен
± ¥, то этот несобственный интеграл называется Расходящимся.

Если F (X ) ≥ 0 для всех X ≥ A , то У несобственного интеграла (6.1) имеется очевидный геометрический смысл, вытекающий из геометрического смысла (4.3) обычного определенного интеграла. Действительно, согласно рис. 5.14

(6.2)

(6.3)

Здесь S ¥ - площадь бесконечно протяженной в направлении оси Ох криволинейной трапеции (рис. 5.15). Несмотря на свою бесконечную протяженность, она может оказаться и конечной. Но это может произойти, согласно рис. 5.15, лишь в случае, когда Y = F (X ) → 0 при X → ¥ . Да и то, если функция Y = F (X ) → 0 при X → ¥ достаточно быстро.

Пример 1. Найти площадь S ¥ , изображенную на рис. 5.16.

,
так как lnB → ¥ при B → ¥ .

Итак, S ¥ = ¥. И это несмотря на то, что функция при X → ¥ . Несобственный интеграл , а значит, он расходится.

Пример 2. Найти площадь S ¥ , изображенную на рис. 5.17.

Здесь S ¥ = 1. То есть бесконечно протяженная площадь оказалась конечной. Это произошло потому, что подинтегральная функция при X → ¥ достаточно быстро (по крайней мере, гораздо быстрее, чем подинтегральная функция в предыдущем примере). Несобственный интеграл (число), а значит, он сходится.

Пример 3 . Выяснить, сходится или расходится несобственный интеграл .

Решение . Вычислим это интеграл:

Не существует. Это очевидно, если вспомнить поведение графика функции Y = = SinX (синусоиды) при X → ¥ . Таким образом, не существует, а значит, он расходится. Впрочем, это и не могло быть иначе, ибо подинтегральная функция cosX не стремится к нулю при Х → ¥ .

Заметим, что при вычислении несобственных интегралов типа , как и при вычислении обычных определенных интегралов , можно сразу применять формулу Ньютона-Лейбница:

Действительно:

Если значение F (¥ ) существует и конечно, то согласно формуле (6.4) Ньютона-Лейбница сходится и несобственный интеграл .

Примечание. Совершенно аналогично интегралам с бесконечным верхним пределом можно рассматривать несобственные интегралы с бесконечным нижним пределом и даже с обоими бесконечными пределами интегрирования. То есть интегралы вида

Для их вычисления тоже можно применять формулу Ньютона-Лейбница.

Пример 4.

Итак, (число), то есть этот интеграл сходится. Его величина π равна площади S ¥ бесконечно протяженной в обе стороны фигуры, изображенной на рис. 5.18.

Заметим, что сам факт сходимости-расходимости несобственных интегралов с бесконечными пределами интегрирования не обязательно устанавливать с помощью прямого вычисления этих интегралов. Это вопрос часто можно решить и гораздо проще, сравнив данный несобственный интеграл с каким-либо другим, для которого сходимость-расходимость уже установлена.

Пусть, например, для всех имеет место неравенство F (X ) £ G (X ), Где Y = F (X ) И Y = G (X ) - Две непрерывные и неотрицательные функции (рис. 5.19). Тогда очевидно, что

Из неравенства (6.6) и рис. 5.19 очевидным образом следует так называемый Признак сравнения несобственных интегралов :

В качестве функции G (X ) , с которой на промежутке Сравнивают данную функцию F (X ), часто используют функцию , а в качестве интеграла сравнения - интеграл , учитывая при этом, что при A > 0 и любых α функция - положительная и непрерывная функция, и что

Пример 5.

Решение. Очевидно, что для всех X Î , а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.

Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f (x ) находится выше оси Ox , определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f (x ) , осью абсцисс и ординатами x = a , x = b . В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x ) (на рисунке ниже - красного цвета), x = a и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:

Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.

Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае - расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.

Несобственные интегралы первого рода - с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.

Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т.е.

.

Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.

Пример 1. Вычислить несобственный интеграл (если он сходится).

Решение. На основании определения несобственного интеграла находим

Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.

В следующем примере подынтегральная функция почти как в примере 1, только степень икса - не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?

Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).

Решение. Предположим сначала, что , тогда

В полученном выражении перейдём к пределу при :

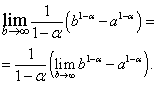
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .

В первом случае, то есть при имеет место . Если , то и не существует.

Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .

Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:

.

Это обобщённая формула Ньютона-Лейбница.

Пример 3. Вычислить несобственный интеграл (если он сходится).

Предел этого интеграла существует:

Второй интеграл, составляющий сумму, выражающую исходный интеграл:

Предел этого интеграла также существует:

.

Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:

Несобственные интегралы второго рода - от неограниченных функций и их сходимость

Пусть функция f (x ) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b , в то время как во всех остальных точках отрезка она непрерывна.

Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.

.

Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае - расходящимся.

Используя формулу Ньютона-Лейбница, выводим.

Рассмотрим два вида несобственных интервалов:

• 1. Несобственные интегралы I-го рода с бесконечными пределами интегрирования;
• 2. Несобственные интегралы II-го рода от функций с бесконечными разрывами.

Несобственные интегралы первого рода с бесконечными пределами интегрирования

Определение: Интегралы вида: называются несобственными интегралами I-го рода с бесконечными пределами, которые определяются с помощью пределов:

Определение Несобственные интегралы называются сходящимися, если существуют конечные пределы, с помощью которых эти интегралы определяются.

Несобственные интегралы называются расходящимися, если эти пределы не существуют или бесконечные.

Действительно, пусть функция f(x) определена и непрерывна при любом значении x=в из полубесконечного отрезка функций имеем:

Он сходится к 1. Тогда согласно теореме 1 несобственный интеграл от меньшей функции: также сходится и его значение меньше 1.

Теорема 2. Если для знакоположительных функций, для которых выполняется неравенство 0?g(x)?f(x), при любых х? а, несобственный интеграл от меньшей функции расходится, то расходится и несобственный интеграл от большей функции.

Пример. Исследовать сходимость интеграла:

Решение. Сравним подинтегральную функцию с функцией. Для знакоположительных на интервале нарушается требование произвольного выбора точки на частичных отрезках – нельзя выбрать =с , поскольку значение функции в этой точке не определено. Однако и для этих случаев можно обобщить понятие определенного интеграла, введя еще один предельный переход. Интегралы по бесконечным промежуткам и от разрывных (неограниченных) функций называют несобственными .

Определение.

Пусть функция
определена на промежутке [a ; ) и интегрируема на любом конечном отрезке [a ; b ], т.е. существует
для любого b > a . Предел вида
называют несобственным интегралом первого рода (или несобственным интегралом по бесконечному промежутку) и обозначают
.

Таким образом, по определению,
=
.

Если предел справа существует и конечен, то несобственный интеграл
называют сходящимся . Если этот предел бесконечен, или не существует вообще, то говорят, что несобственный интеграл расходится .

Аналогично можно ввести понятие несобственного интеграла от функции
по промежутку (–; b ]:

=
.

А несобственный интеграл от функции
по промежутку (–; +) определяется как сумма введенных выше интегралов:

=
+
,

где а – произвольная точка. Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно из слагаемых.

С геометрической точки зрения, интеграл
,
, определяет численное значение площади бесконечной криволинейной трапеции, ограниченной сверху графиком функции
, слева – прямой
, снизу – осью ОХ. Сходимость интеграла означает существование конечной площади такой трапеции и равенство ее пределу площади криволинейной трапеции с подвижной правой стенкой
.

На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница :

=
= F(+ ) – F(a ),

где F(+ ) =
. Если этот предел существует, то интеграл сходится, в противном случае – расходится.

Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.

Рассмотрим теперь обобщение для случая неограниченной функции.

Определение

Пусть функция
определена на промежутке [a ; b ), неограниченна в некоторой окрестности точки b , и непрерывна на любом отрезке
, где >0 (и, следовательно, интегрируема на этом отрезке, т.е.
существует). Предел вида
называется несобственным интегралом второго рода (или несобственным интегралом от неограниченной функции) и обозначается
.

Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению

=
.

Если предел справа существует и конечен, то интеграл называется сходящимся . Если конечного предела не существует, то несобственный интеграл называется расходящимся.

Аналогично можно определить несобственный интеграл от функции
имеющей бесконечный разрыв в точке а :

=
.

Если функция
имеет бесконечный разрыв во внутренней точке с 
, то несобственный интеграл определяется следующим образом

=
+
=
+
.

Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.

С геометрической точки зрения, несобственный интеграл от неограниченной функции также характеризует площадь неограниченной криволинейной трапеции:

Поскольку несобственный интеграл выводится путем предельного перехода из определенного интеграла, то все свойства определенного интеграла могут быть перенесены (с соответствующими уточнениями) на несобственные интеграла первого и второго рода.

Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости . Признаки сходимости несобственных интегралов:

1) Признак сравнения .

Пусть для всех х 

. Тогда, если
сходится, то сходится и
, причем

. Если
расходится, то расходится и
.

2) Если сходится
, то сходится и
(последний интеграл в этом случае называется абсолютно сходящимся ).

Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.

Примеры решения задач.

Пример 1.

а)
; б)
; в)

г)
; д)
.

Решение.

а) По определению имеем:

.

б) Аналогично

Следовательно, данный интеграл сходится и равен .

в) По определению
=
+
, причем, а – произвольное число. Положим в нашем случае
, тогда получим:

Данный интеграл сходится.

Значит, данный интеграл расходится.

д) Рассмотрим
. Чтобы найти первообразную подынтегральной функции, необходимо применить метод интегрирования по частям. Тогда получим:

Поскольку ни
, ни
не существуют, то не существует и

Следовательно, данный интеграл расходится.

Пример 2.

Исследовать сходимость интеграла в зависимости от п .

Решение.

При
имеем:

Если
, то
и . Следовательно, интеграл расходится.

Если
, то
, а
, тогда

= ,

Следовательно, интеграл сходится.

Если
, то

следовательно, интеграл расходится.

Таким образом,

Пример 3.

Вычислить несобственный интеграл или установить его расходимость:

а)
; б)
; в)
.

Решение.

а) Интеграл
является несобственным интегралом второго рода, поскольку подынтегральная функция
не ограничена в точке

. Тогда, по определению,

.

Интеграл сходится и равен .

б) Рассмотрим
. Здесь также подынтегральная функция не ограничена в точке
. Поэтому, данный интеграл – несобственный второго рода и по определению,

Следовательно, интеграл расходится.

в) Рассмотрим
. Подынтегральная функция
терпит бесконечный разрыв в двух точках:
и
, первая из которых принадлежит промежутку интегрирования
. Следовательно, данный интеграл – несобственный второго рода. Тогда, по определению

=

=

.

Следовательно, интеграл сходится и равен
.