Презентация и урок на тему: "Рациональные уравнения. Алгоритм и примеры решения рациональных уравнений"

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине "Интеграл" для 8 класса
Пособие к учебнику Макарычева Ю.Н. Пособие к учебнику Мордковича А.Г.

Знакомство с иррациональными уравнениями

Ребята, мы научились решать квадратные уравнения. Но математика только ими не ограничивается. Сегодня мы научимся решать рациональные уравнения. Понятие рациональных уравнений во многом схоже с понятием рациональных чисел. Только помимо чисел теперь у нас введена некоторая переменная $х$. И таким образом мы получаем выражение, в котором присутствуют операции сложения, вычитания, умножения, деления и возведения в целую степень.

Пусть $r(x)$ – это рациональное выражение . Такое выражение может представлять из себя простой многочлен от переменной $х$ или отношение многочленов (вводится операция деления, как для рациональных чисел).
Уравнение $r(x)=0$ называется рациональным уравнением .
Любое уравнение вида $p(x)=q(x)$, где $p(x)$ и $q(x)$ – рациональные выражения, также будет являться рациональным уравнением .

Рассмотрим примеры решения рациональных уравнений.

Пример 1.
Решить уравнение: $\frac{5x-3}{x-3}=\frac{2x-3}{x}$.

Решение.
Перенесем все выражения в левую часть: $\frac{5x-3}{x-3}-\frac{2x-3}{x}=0$.
Если бы в левой части уравнения были представлены обычные числа, то мы бы привели две дроби к общему знаменателю.
Давайте так и поступим: $\frac{(5x-3)*x}{(x-3)*x}-\frac{(2x-3)*(x-3)}{(x-3)*x}=\frac{5x^2-3x-(2x^2-6x-3x+9)}{(x-3)*x}=\frac{3x^2+6x-9}{(x-3)*x}=\frac{3(x^2+2x-3)}{(x-3)*x}$.
Получили уравнение: $\frac{3(x^2+2x-3)}{(x-3)*x}=0$.

Дробь равна нулю, тогда и только тогда, когда числитель дроби равен нулю, а знаменатель отличен от нуля. Тогда отдельно приравняем числитель к нулю и найдем корни числителя.
$3(x^2+2x-3)=0$ или $x^2+2x-3=0$.
$x_{1,2}=\frac{-2±\sqrt{4-4*(-3)}}{2}=\frac{-2±4}{2}=1;-3$.
Теперь проверим знаменатель дроби: $(x-3)*x≠0$.
Произведение двух чисел равно нулю, когда хотя бы одно из этих чисел равно нулю. Тогда: $x≠0$ или $x-3≠0$.
$x≠0$ или $x≠3$.
Корни, полученные в числителе и знаменателе, не совпадают. Значит в ответ записываем оба корня числителя.
Ответ: $х=1$ или $х=-3$.

Если вдруг, один из корней числителя совпал с корнем знаменателя, то его следует исключить. Такие корни называются посторонними!

Алгоритм решения рациональных уравнений:

1. Все выражения, содержащиеся в уравнении, перенести в левую сторону от знака равно.
2. Преобразовать эту часть уравнения к алгебраической дроби: $\frac{p(x)}{q(x)}=0$.
3. Приравнять полученный числитель к нулю, то есть решить уравнение $p(x)=0$.
4. Приравнять знаменатель к нулю и решить полученное уравнение. Если корни знаменателя совпали с корнями числителя, то их следует исключить из ответа.

Пример 2.
Решите уравнение: $\frac{3x}{x-1}+\frac{4}{x+1}=\frac{6}{x^2-1}$.

Решение.
Решим согласно пунктам алгоритма.
1. $\frac{3x}{x-1}+\frac{4}{x+1}-\frac{6}{x^2-1}=0$.
2. $\frac{3x}{x-1}+\frac{4}{x+1}-\frac{6}{x^2-1}=\frac{3x}{x-1}+\frac{4}{x+1}-\frac{6}{(x-1)(x+1)}= \frac{3x(x+1)+4(x-1)-6}{(x-1)(x+1)}=$ $=\frac{3x^2+3x+4x-4-6}{(x-1)(x+1)}=\frac{3x^2+7x-10}{(x-1)(x+1)}$.
$\frac{3x^2+7x-10}{(x-1)(x+1)}=0$.
3. Приравняем числитель к нулю: $3x^2+7x-10=0$.
$x_{1,2}=\frac{-7±\sqrt{49-4*3*(-10)}}{6}=\frac{-7±13}{6}=-3\frac{1}{3};1$.
4. Приравняем знаменатель к нулю:
$(x-1)(x+1)=0$.
$x=1$ и $x=-1$.
Один из корней $х=1$ совпал с корнем из числителя, тогда мы его в ответ не записываем.
Ответ: $х=-1$.

Решать рациональные уравнения удобно с помощью метода замены переменных. Давайте это продемонстрируем.

Пример 3.
Решить уравнение: $x^4+12x^2-64=0$.

Решение.
Введем замену: $t=x^2$.
Тогда наше уравнение примет вид:
$t^2+12t-64=0$ - обычное квадратное уравнение.
$t_{1,2}=\frac{-12±\sqrt{12^2-4*(-64)}}{2}=\frac{-12±20}{2}=-16; 4$.
Введем обратную замену: $x^2=4$ или $x^2=-16$.
Корнями первого уравнения является пара чисел $х=±2$. Второе - не имеет корней.
Ответ: $х=±2$.

Пример 4.
Решить уравнение: $x^2+x+1=\frac{15}{x^2+x+3}$.
Решение.
Введем новую переменную: $t=x^2+x+1$.
Тогда уравнение примет вид: $t=\frac{15}{t+2}$.
Дальше будем действовать по алгоритму.
1. $t-\frac{15}{t+2}=0$.
2. $\frac{t^2+2t-15}{t+2}=0$.
3. $t^2+2t-15=0$.
$t_{1,2}=\frac{-2±\sqrt{4-4*(-15)}}{2}=\frac{-2±\sqrt{64}}{2}=\frac{-2±8}{2}=-5; 3$.
4. $t≠-2$ - корни не совпадают.
Введем обратную замену.
$x^2+x+1=-5$.
$x^2+x+1=3$.
Решим каждое уравнение по отдельности:
$x^2+x+6=0$.
$x_{1,2}=\frac{-1±\sqrt{1-4*(-6)}}{2}=\frac{-1±\sqrt{-23}}{2}$ - нет корней.
И второе уравнение: $x^2+x-2=0$.
Корнями данного уравнения будут числа $х=-2$ и $х=1$.
Ответ: $х=-2$ и $х=1$.

Пример 5.
Решить уравнение: $x^2+\frac{1}{x^2} +x+\frac{1}{x}=4$.

Решение.
Введем замену: $t=x+\frac{1}{x}$.
Тогда:
$t^2=x^2+2+\frac{1}{x^2}$ или $x^2+\frac{1}{x^2}=t^2-2$.
Получили уравнение: $t^2-2+t=4$.
$t^2+t-6=0$.
Корнями данного уравнения является пара:
$t=-3$ и $t=2$.
Введем обратную замену:
$x+\frac{1}{x}=-3$.
$x+\frac{1}{x}=2$.
Решим по отдельности.
$x+\frac{1}{x}+3=0$.
$\frac{x^2+3x+1}{x}=0$.
$x_{1,2}=\frac{-3±\sqrt{9-4}}{2}=\frac{-3±\sqrt{5}}{2}$.
Решим второе уравнение:
$x+\frac{1}{x}-2=0$.
$\frac{x^2-2x+1}{x}=0$.
$\frac{(x-1)^2}{x}=0$.
Корнем этого уравнения является число $х=1$.
Ответ: $x=\frac{-3±\sqrt{5}}{2}$, $x=1$.

Задачи для самостоятельного решения

Решить уравнения:

1. $\frac{3x+2}{x}=\frac{2x+3}{x+2}$.

2. $\frac{5x}{x+2}-\frac{20}{x^2+2x}=\frac{4}{x}$.
3. $x^4-7x^2-18=0$.
4. $2x^2+x+2=\frac{8}{2x^2+x+4}$.
5. $(x+2)(x+3)(x+4)(x+5)=3$.

Муниципальное общеобразовательное учреждение

Средняя общеобразовательная школа №21

Рациональные уравнения.

(8 класс)

Учитель математики:

Квасницкая И.В.

Ковров,

2010-2011

Тема: Рациональные уравнения.

Цель: Формирование навыков решения рациональных уравнений.

Задачи: - формирование понятия «Рациональное уравнение»;

Формирование навыков решения рациональных уравнений различными способами;

Совершенствование навыков преобразования алгебраических дробей;

Совершенствование навыков применения формул сокращенного умножения в преобразовании алгебраических дробей;

Совершенствование навыков устного счета;

Развитие мыслительных операций;

Воспитание грамотной математической речи, аккуратности;

Воспитание сотрудничества, взаимопомощи.

План урока:

1. Самоопределение к учебной деятельности.

2. Актуализация знаний и фиксация затруднения в деятельности.

3. Выявление причины затруднения и постановка цели деятельности.

4. Построение проекта выхода из затруднения.

5. Первичное закрепление во внешней речи.

6. Самостоятельная работа с самопроверкой по эталону.

7. Включение в систему знаний и повторение.

8. Рефлексия деятельности на уроке.

9. Домашнее задание.

Ход урока.

Оборудование, демонстрационный материал:

1) задания для актуализации знаний

№ 1 ··

№2
+
:
-

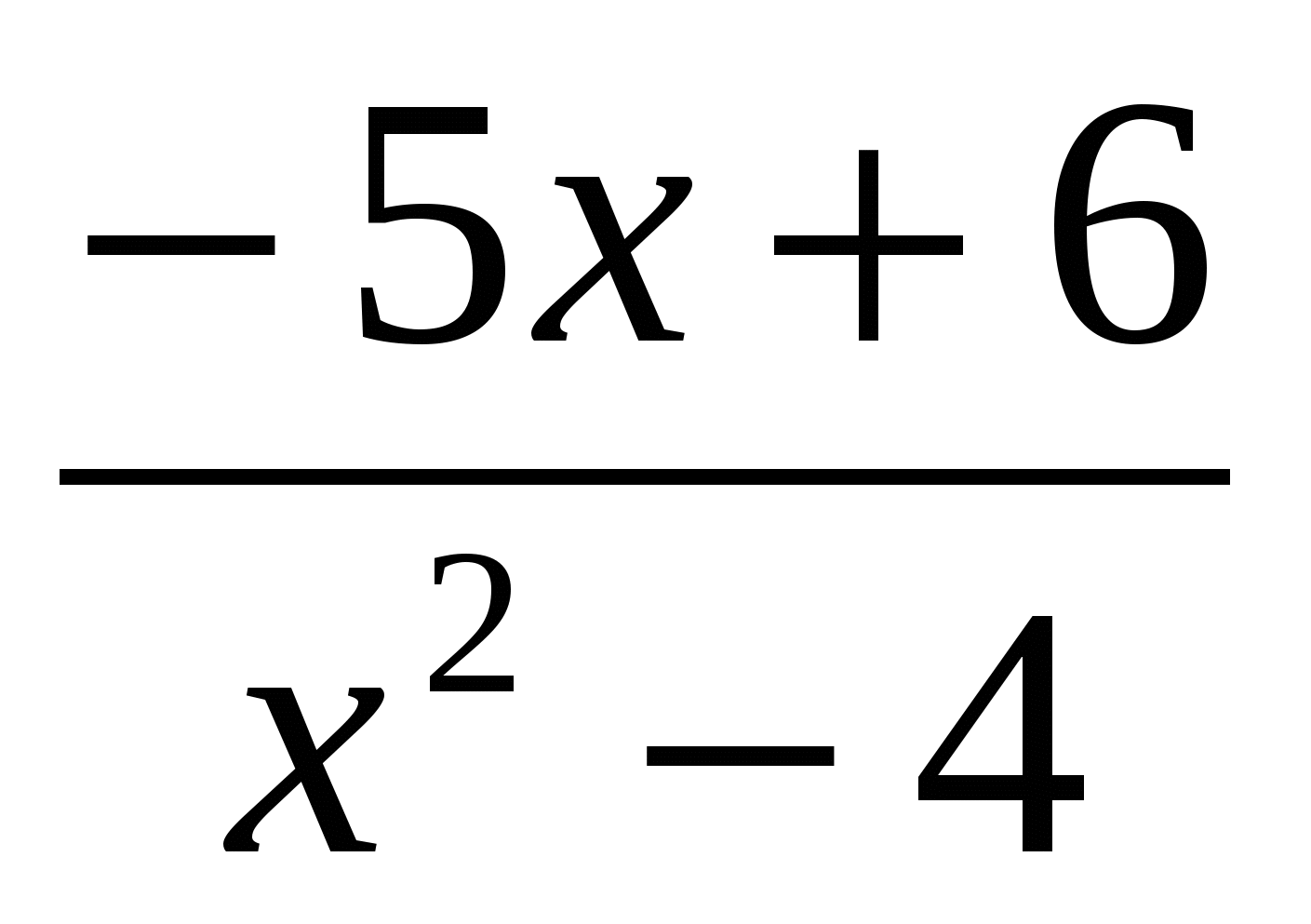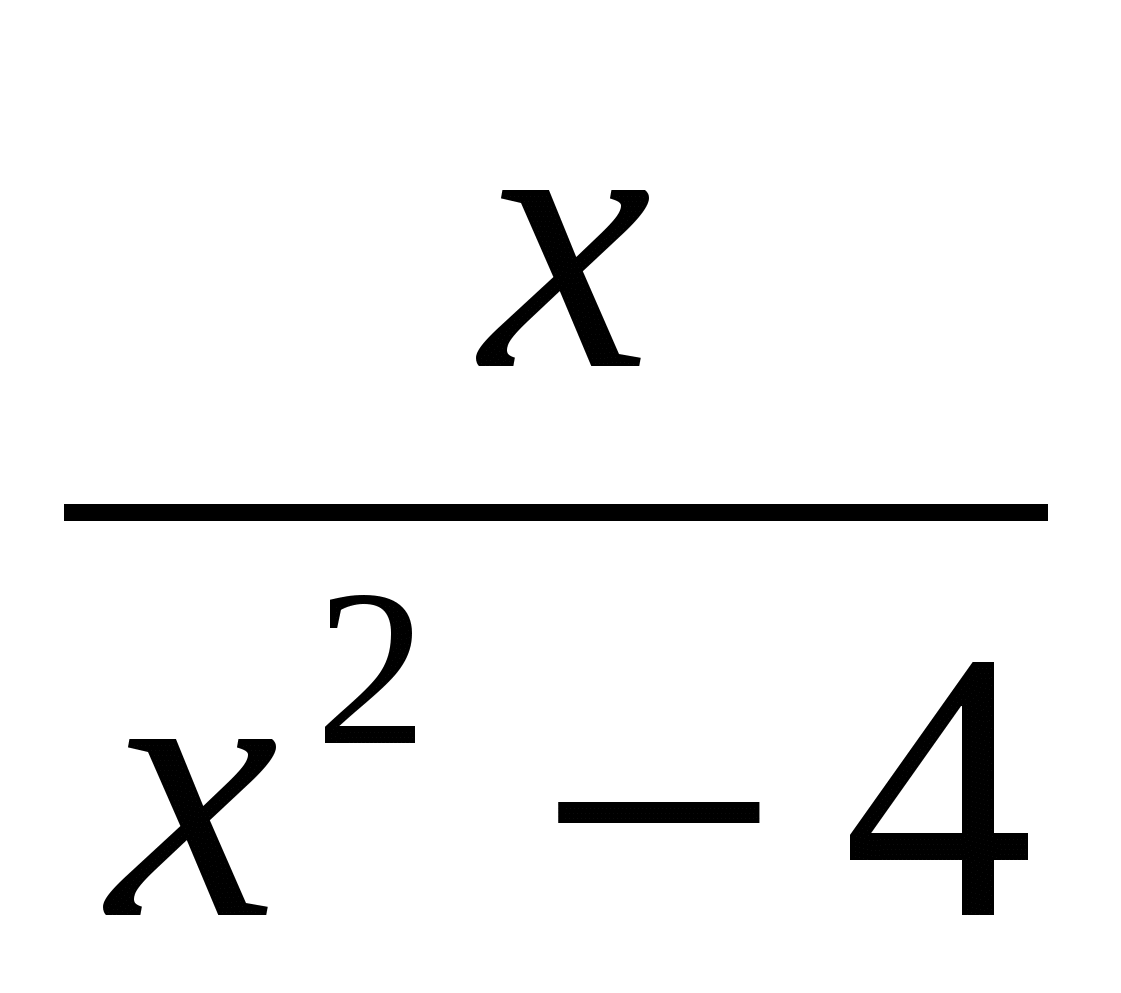№ 3
-2х=
+

№ 4
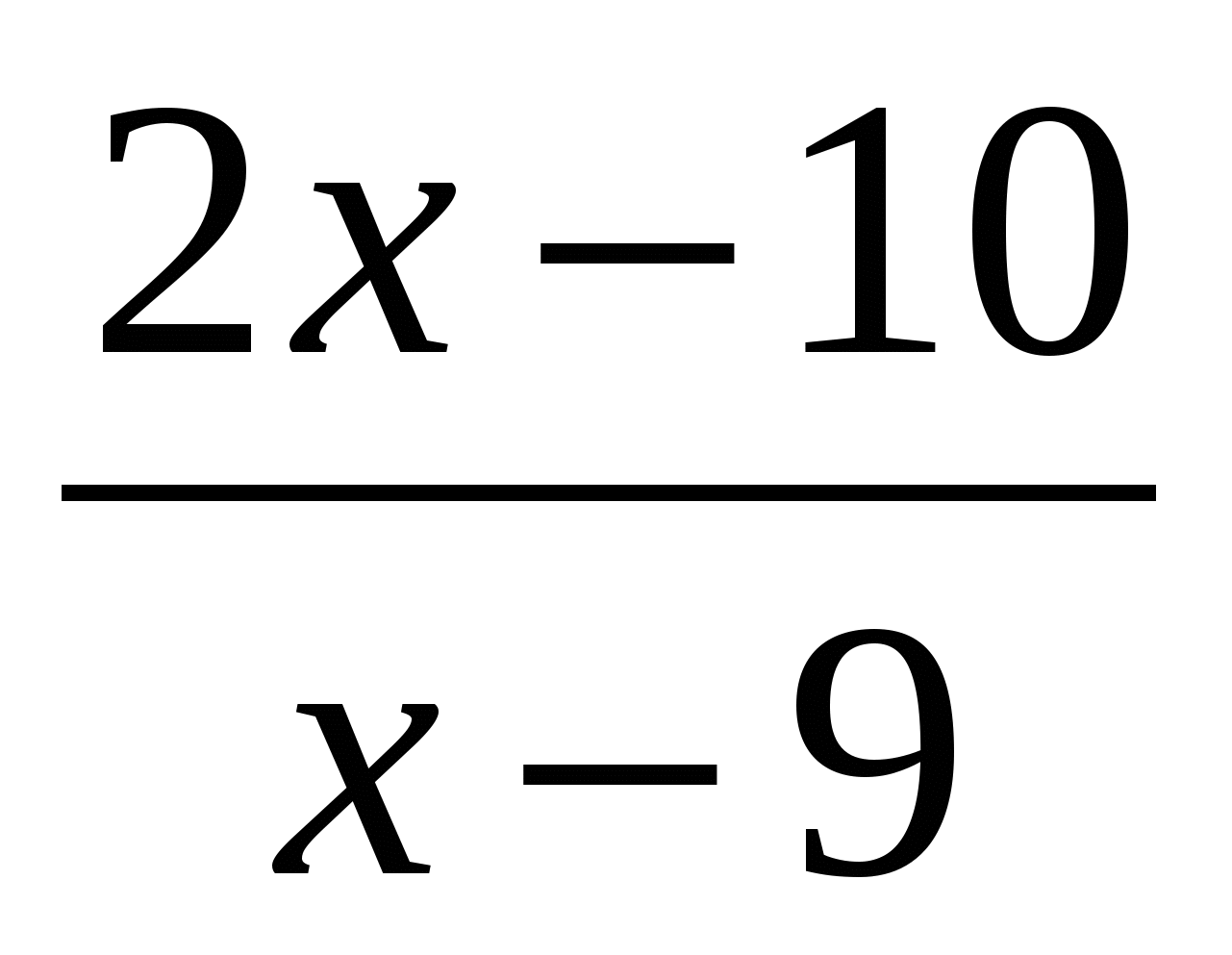=0.

2) Алгоритм решения уравнений

1) Привести дроби к общему знаменателю в левой и правой частях уравнения.

2) Воспользоваться правилами:

а) равенства дроби нулю;

б) свойствами пропорции;

в) равенства дробей.

3) Алгоритм решения рациональных уравнений

а) равенства дроби нулю;

б) свойствами пропорции;

в) равенства дробей.

4) Задание для первичного закрепления во внешней речи

-
=
,

-
=,

+
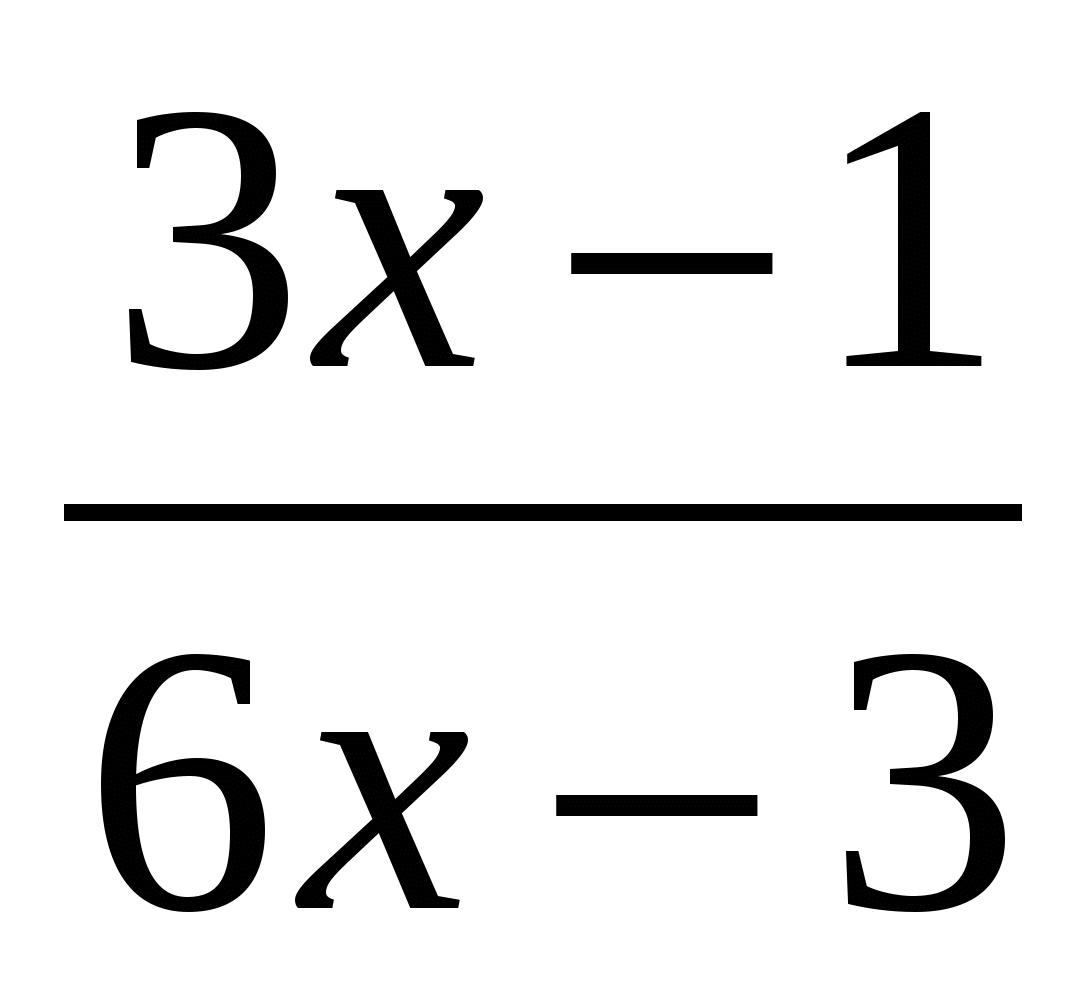=, | ·3(2х-1)(2х+1)

(2х+1)(3х-1)+3=3(2х-1)х,

6х 2 -2х+3х-1+3=6х 2 -3х,

5) образец выполнения задания в парах

№ 250(б)

=
,

О.Д.З.: х≠2,

2- не входит в О.Д.З.

Ответ. Корней нет

6) эталон для самопроверки самостоятельной работы

+
=0,

О.Д.З.: t ≠1,6; t≠,

=0,

=0,

46t+46=0,

t=1- входит в О.Д.З.

Ответ. 1.

Ход урока

1. Самоопределение к учебной деятельности

– Здравствуйте! Какую тему мы изучали на прошлых уроках? (Преобразование рациональных выражений.)

– На прошлых уроках вы многому научились, и эти знания помогут сегодня совершить новое «открытие».

2. Актуализация знаний и фиксация затруднения в деятельности

Цель этапа:

1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: действия с алгебраическими дробями;

2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;

3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;

4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний: решить рациональное уравнение.

Организация учебного процесса на этапе 2:

1. На доске: ··

От значения каких переменных не зависит значение выражения? Укажите все допустимые значения переменных.

2. На доске: +:-

Назовите порядок действий. Какую формулу сокращенного умножения примените для разложения на множители двучлена, находящегося в знаменателе 1 дроби? В тетради выполните 1-ое действие. (На закрытой доске 1 ученик.)

Итак, какой ответ получился? Все ли получили такой ответ? Какое действие необходимо выполнить вторым? Можно ли выполнить одновременно сложение и вычитание алгебраических дробей? Не повлияет ли это на результат?

Пожалуйста, выполните 2 действие, свой ответ сверьте с ответом на доске. (Работа в парах ).

3. Задание группам. Решите уравнение: -2х=+

Каким алгоритмом пользовались при решении? (формулируют, вывесить на доску. Рассмотреть различные способы решения )

4. - Решите равнение: =0. В чем отличие данного уравнения от предыдущего? (в знаменателе переменная). Знаете способ его решения? (Нет).

3. Выявление причины затруднения и постановка цели деятельности

Цель этапа:

1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;

2) согласовать цель и тему урока.

Организация учебного процесса на этапе 3:

Что собою представляет левая часть данного уравнения? Что собою представляет правая часть данного уравнения? Как называются уравнения такого вида? (Рациональное уравнение)

Тема. Цель. (Ученики формулируют сами. )

Так какое уравнение называют рациональным? (учащиеся формулируют ) Сравните с определением в учебнике.

4. Построение проекта выхода из затруднения

Цель этапа:

1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;

2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью алгоритма.

Организация учебного процесса на этапе 4:

Как вы думаете, почему возникло затруднение при решении заданного уравнения? (Не знаем способы его решения.)

Какие предложения у Вас появились? (Воспользоваться свойством равенства нулю дроби: (х-9) не может быть равно нулю, поэтому (2х-10) равно 0, откуда находим х=5.)

Задание группам. Решите уравнение: =
-

Каким алгоритмом решения вы пользовались? (что и в начале урока).

Есть ли отличие при решении данного рационального уравнения от того, которое было решено в начале урока? (Да, необходимо помнить о том, что знаменатель дроби не может быть равен нулю, то есть найти область допустимых значений переменной.)

Нужно ли эту особенность внести в алгоритм решения рациональных уравнений? (Конечно.)

-

1) Разложить знаменатель на множители.

2) Найти область допустимых значений переменной.

3) Привести дроби к общему знаменателю в левой и правой частях уравнения.

4) Воспользоваться правилами:

а) равенства дроби нулю;

б) свойствами пропорции;

в) равенства дробей.

Сформулируйте алгоритм решения рациональных уравнений. (Алгоритм вывесить на доску.)

6. Самостоятельная работа с самопроверкой по эталону

Цель этапа:

проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.

Организация учебного процесса на этапе 6:

Работы проверяются по эталону. Ошибки исправляются, анализируются, выясняется их причина.

7. Включение в систему знаний и повторение

Цель этапа:

Тренировать навыки использования нового содержания совместно с ранее изученным: решение задач с помощью системы уравнений;

Организация учебного процесса на этапе 7:

№241.(Устно.)

8. Рефлексия деятельности на уроке

Цель этапа:

1) зафиксировать новое содержание, изученное на уроке;

2) оценить собственную деятельность на уроке;

3) поблагодарить одноклассников, которые помогли получить результат урока;

4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;

5) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 8:

– Что нового узнали на уроке?

– Что использовали для «открытия» нового знания?

– Проанализируйте свою работу на уроке.

Домашнее задание

§ 1 Целое и дробное рациональные уравнение

В этом уроке разберем такие понятия, как рациональное уравнение, рациональное выражение, целое выражение, дробное выражение. Рассмотрим решение рациональных уравнений.

Рациональным уравнением называют уравнение, в котором левая и правая части являются рациональными выражениями.

Рациональные выражения бывают:

Дробные.

Целое выражение составлено из чисел, переменных, целых степеней с помощью действий сложения, вычитания, умножения, а также деления на число, отличное от нуля.

Например:

В дробных выражениях есть деление на переменную или выражение с переменной. Например:

Дробное выражение не при всех значениях входящих в него переменных имеет смысл. Например, выражение

при х = -9 не имеет смысла, так как при х = -9 знаменатель обращается в нуль.

Значит, рациональное уравнение может быть целым и дробным.

Целое рациональное уравнение - это рациональное уравнение, в котором левая и правая части - целые выражения.

Например:

Дробное рациональное уравнение - это рациональное уравнение, в котором или левая, или правая части - дробные выражения.

Например:

§ 2 Решение целого рационального уравнения

Рассмотрим решение целого рационального уравнения.

Например:

Умножим обе части уравнения на наименьший общий знаменатель знаменателей входящих в него дробей.

Для этого:

1. найдем общий знаменатель для знаменателей 2, 3, 6. Он равен 6;

2. найдем дополнительный множитель для каждой дроби. Для этого общий знаменатель 6 делим на каждый знаменатель

дополнительный множитель для дроби

дополнительный множитель для дроби

3. умножим числители дробей на соответствующие им дополнительные множители. Таким образом, получим уравнение

которое равносильно данному уравнению

Слева раскроем скобки, правую часть перенесем налево, изменив знак слагаемого при переносе на противоположный.

Приведем подобные члены многочлена и получим

Видим, что уравнение линейное.

Решив его, найдем, что х = 0,5.

§ 3 Решение дробного рационального уравнения

Рассмотрим решение дробного рационального уравнения.

Например:

1.Умножим обе части уравнения на наименьший общий знаменатель знаменателей входящих в него рациональных дробей.

Найдем общий знаменатель для знаменателей х + 7 и х - 1.

Он равен их произведению (х + 7)(х - 1).

2.Найдем дополнительный множитель для каждой рациональной дроби.

Для этого общий знаменатель (х + 7)(х - 1) делим на каждый знаменатель. Дополнительный множитель для дроби

равен х - 1,

дополнительный множитель для дроби

равен х+7.

3.Умножим числители дробей на соответствующие им дополнительные множители.

Получим уравнение (2х - 1)(х - 1) = (3х + 4)(х + 7), которое равносильно данному уравнению

4.Слева и справа умножим двучлен на двучлен и получим следующее уравнение

5.Правую часть перенесем налево, изменив знак каждого слагаемого при переносе на противоположный:

6.Приведем подобные члены многочлена:

7.Можно обе части разделить на -1. Получим квадратное уравнение:

8.Решив его, найдем корни

Так как в уравнении

левая и правая части - дробные выражения, а в дробных выражениях при некоторых значениях переменных знаменатель может обратиться в нуль, то необходимо проверить, не обращается ли в нуль при найденных х1 и х2 общий знаменатель.

При х = -27 общий знаменатель (х + 7)(х - 1) не обращается в нуль, при х = -1 общий знаменатель также не равен нулю.

Следовательно, оба корня -27 и -1 являются корнями уравнения.

При решении дробного рационального уравнения лучше сразу указать область допустимых значений. Исключить те значения, при которых общий знаменатель обращается в нуль.

Рассмотрим еще один пример решения дробного рационального уравнения.

Например, решим уравнение

Знаменатель дроби правой части уравнения разложим на множители

Получим уравнение

Найдем общий знаменатель для знаменателей (х - 5), х, х(х - 5).

Им будет выражение х(х - 5).

теперь найдем область допустимых значений уравнения

Для этого общий знаменатель приравняем к нулю х(х - 5) = 0.

Получим уравнение, решив которое, найдем, что при х = 0 или при х = 5 общий знаменатель обращается в нуль.

Значит, х = 0 или х = 5 не могут быть корнями нашего уравнения.

Теперь можно найти дополнительные множители.

Дополнительным множителем для рациональной дроби

дополнительным множителем для дроби

будет (х - 5),

а дополнительный множитель дроби

Числители умножим на соответствующие дополнительные множители.

Получим уравнение х(х - 3) + 1(х - 5) = 1(х + 5).

Раскроем скобки слева и справа, х2 - 3х + х - 5 = х + 5.

Перенесем слагаемые справа налево, изменив знак переносимых слагаемых:

Х2 - 3х + х - 5 - х - 5 = 0

И после приведения подобных членов получим квадратное уравнение х2 - 3х - 10 = 0. Решив его, найдем корни х1 = -2; х2 = 5.

Но мы уже выяснили, что при х = 5 общий знаменатель х(х - 5) обращается в нуль. Следовательно, корнем нашего уравнения

будет х = -2.

§ 4 Краткие итоги урока

Важно запомнить:

При решении дробных рациональных уравнений надо поступить следующим образом:

1.Найти общий знаменатель дробей входящих в уравнение. При этом если знаменатели дробей можно разложить на множители, то разложить их на множители и затем найти общий знаменатель.

2.Умножить обе части уравнения на общий знаменатель: найти дополнительные множители, умножить числители на дополнительные множители.

3.Решить получившееся целое уравнение.

4.Исключить из его корней те, которые обращают в нуль общий знаменатель.

Список использованной литературы:

1. Макарычев Ю.Н., Н. Г. Миндюк, Нешков К.И., Суворова С.Б. / Под редакцией Теляковского С.А. Алгебра: учебн. для 8 кл. общеобразоват. учреждений. - М.: Просвещение, 2013.
2. Мордкович А.Г. Алгебра. 8 кл.: В двух частях. Ч.1: Учеб. для общеобразоват. учреждений. - М.: Мнемозина.
3. Рурукин А.Н. Поурочные разработки по алгебре: 8 класс.- М.: ВАКО, 2010.
4. Алгебра 8 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворовой / Авт.-сост. Т.Л. Афанасьева, Л.А. Тапилина. -Волгоград: Учитель, 2005.

На данном уроке будет рассмотрено решение рациональных уравнений. С помощью рациональных уравнений решается целый ряд задач, которые возникают не только на страницах учебника математики, но и в жизни. Однако, для того чтобы решить рациональное уравнение, его ещё необходимо уметь правильно составить. Поэтому на данном уроке мы не только рассмотрим примеры решения рациональных уравнений как таковых, но и примеры математического моделирования задачи, которое приводит к возникновению соответствующих рациональных уравнений.

Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями

Урок: Решение рациональных уравнений

Как вы уже успели заметить на предыдущем уроке, основа решения рациональных уравнений - техника преобразования рациональных выражений. Рассмотрим пример решения рационального уравнения.

Пример 1

Решить уравнение: .

Решение:

В первую очередь обратим внимание на то, что в числителях обеих дробей, а также в правой части уравнения стоят чётные числа. То есть, можно упростить уравнение, поделив обе его части на . Этот шаг не является обязательным, но, чем проще уравнение, тем легче его решать, а чем меньше числа, фигурирующие в уравнении, тем легче арифметические вычисления при его решении.

В результате сокращения получаем:

Теперь перенесём все члены уравнения в левую часть, чтобы получить справа , а затем приведём полученные в левой части дроби к общему знаменателю:

Напомним, что дробь равна тогда и только тогда, когда её числитель равен , а знаменатель не равен . Поэтому наше уравнение превращается в следующую систему:

Теперь вспомним ещё один важный факт: произведение равно тогда и только тогда, когда хотя бы один из его множителей равен , а остальные множители при этом существуют. И наша система превращается в следующую:

.

Оба полученных корня являются решениями данного уравнения, так как при них знаменатель определён.

Рассмотренное нами уравнение является моделью для такой задачи:

Задача 1

Лодка прошла по течению реки и против течения реки, затратив на весь путь . Чему равна собственная скорость лодки, если скорость течения реки равна ?

Решение:

Решение данной задачи осуществим с помощью метода математического моделирования и выделим 3 этапа данного метода.

Этап 1. Составление математической модели

Обозначим через собственную скорость лодки (это стандартный приём при решении текстовых задач - обозначить с помощью неизвестной ту величину, которая спрашивается в условии задачи). Тогда:

Скорость движения лодки по течению реки;

Скорость движения лодки против течения реки.

В этом случае, воспользовавшись формулой: , получаем, что время движения лодки по течению реки выражается как , а время движения лодки против течения реки - . Тогда общее время движения лодки равно , откуда получаем уравнение:

- это и есть математическая модель данной задачи.

Этап 2. Работа с математической моделью

В данном случае работа с математической моделью сводится к решению данного рационального уравнения, что мы уже сделали в примере 1. При этом получили корни уравнения: .

Этап 3. Ответ на вопрос задачи

Дело в том, что математическая модель потому и является математической, что абстрагирована от реальной жизни. Если брать конкретно данную задачу, то математическая модель - это уравнение, которое может иметь любые корни. Однако неизвестная величина обозначает скорость лодки, поэтому не может быть, к примеру, отрицательной. Или: не может быть меньше скорости течения реки, иначе бы лодка не смогла бы плыть против течения. И такие ограничения могут быть в самых разных задачах. Поэтому, прежде чем записать ответ, необходимо оценить, является ли он правдоподобным.

В данном случае очевидно, что не подходит, так как лодка не смогла бы с такой скоростью плыть против течения. Поэтому в ответ пойдёт только одна величина: .

Ответ:

Рассмотрим несколько примеров на решение непосредственно рациональных уравнений.

Пример 2

Решить уравнение: .

Решение:

Перенесём все слагаемые в левую часть, а затем приведём дроби к общему знаменателю.

Ответ: .

Пример 3

Решить уравнение: .

Решение:

В данном уравнении в правой части уже стоит , поэтому ничего переносить левую часть не нужно. Сразу приведём дроби в левой части к общему знаменателю:

Снова воспользуемся тем фактом, что дробь равна тогда и только тогда, когда её числитель равен , а знаменатель не равен . Из этого следует, что данное уравнение эквивалентно системе:

Подставив данное значение в знаменатель, убеждаемся, что он не равен . Значит, это значение переменной является ответом.

Ответ: .

Пример 4

Решить уравнение: .

Решение:

Схема решения данного уравнения абсолютно такая же, как и у предыдущих:

Ответ: .

К решению рациональных уравнений часто сводятся различные задачи. Рассмотрим один из таких примеров.

Задача 2

Существует ли такое значение , при котором разность дробей и равна ?

МОУ «Ракитянская средняя общеобразовательная школа № 3

имени Н.Н. Федутенко»

Урок алгебры

«Решение дробных рациональных уравнений»

8 класс

Участник конкурса

Учитель математики

Цецорина С.Н.

п. Ракитное – 1

Тип урока: Закрепление знаний и способов действий

Формы работы: Парная, индивидуальная,групповая

Оборудование: 1. Презентация урока

2. Тексты заданий к проверке домашнего задания, работе

в группах, рефлекия

3. Оценочный лист

4. Открытки – мозаика

5. Отрывок песни «Русскому солдату»

Цели урока:

Способствовать выработке умений и навыков решать дробные рациональные уравнения, созданию условий для взаимоконтроля, самоконтроля усвоения знаний и умений;

способствовать закреплению навыка решения линейных уравнений и квадратных уравнений по формуле;

применять приемы: обобщения, сравнения, выделения главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти;

содействовать воспитанию интереса к математике, активности, организованности, умения общаться, любви к родному краю.

Ход урока

Организационный момент

Ребята, сегодня урок алгебры буду вести я. Меня зовут Светлана Николаевна. Я надеюсь, что урок пройдет в теплой дружеской атмосфере и мы, не смотря на все трудности, вместе добьемся цели.

«Уравнение – это золотой ключ,

открывающий все математические

сезамы» (С. Коваль)

И вы наверное поняли, чтобы проникнуть во все математические сезамы, необходимо научиться решать уравнения.

Ребята, тема урока «Дробные рациональные уравнения». Основными задачами являются:

1. Закрепление решения дробных рациональных уравнений, попутно повторить решение квадратных и линейных уравнений.

Я предлагаю следующую последовательность урока:

1. На этапе проверки домашнего задания проведем тестирование по теории и практике.

2. Актуализация знаний пройдет в форме фронтального опроса.

3. Затем Вас ожидает разноуровневая самостоятельная работа.

4. Итогом урока является оформление оценочного листа и выставление полученных Вами оценок.

Проверка домашнего задания.

Для проверки домашнего задания я предлагаю вам ТЕСТ , в котором вы проверите себя по основным правилам. (работа в парах). Каждой паре предлагается 1 задание. Букву правильного ответа вписываем на доске в таблицу.

ТЕСТ

Укажите правильный ответ на вопрос: «Из каких чисел можно извлечь точный квадратный корень?»

а) 64; 0,25; - 4; 7; 1.

с) 64; 0,25; 1.

Укажите квадратное уравнение, записанное в стандартном виде:

а) ах 2 + b х + с = 0;

б) b х + ах 2 + с = 0.

3. Назовите коэффициенты квадратного уравнения 5х 2 – 13х + 9 = 0

х) a = 5 , b = - 13 , c = 9

б) a = 5 , b = 9 , c = - 13

4. Правильно ли составлено уравнение, у которого первый коэффициент

3 , второй коэффициент (- 5) , свободный член 17:

б) - 5х 2 + 3х + 17 = 0;

а) 3х 2 – 5х + 17 = 0

5. Какое из уравнений является дробным рациональным:

р)
.

6. Каков общий знаменатель у дробей:
и

а) (х + 2); б) (х – 2); н) (х + 2) (х – 2)

7. Какова область допустимых значений выражения

а) х
б) х
и х

8. Каковы корни уравнения х (х + 4) = 0

б) х = 0 и х = 4; я) х = 0 и х = - 4.

Задания при проверке показывают на экране.

Учащиеся работают в тетрадях. Получилось слово «Сахарная». Может кто –то знает эту улицу? Сейчас это улица Федутенко в поселке Ракитное -1 (Сахзавод), она получила это название в 1985 году к 40 –летию Победы в ВОВ, в честь Героя Советского Союза, летчицы, Надежды Никифоровны Федутенко, которая жила на этой улице, училась в нашей школе и в 2008 году школе присвоено ее имя. Я рассказала вам об этом не только потому, что я живу на этой улице, работаю в этой школе. А может вы скажите почему я об этом заговорила? Потому, что в этом году будет праздноваться 65 – летие Победы в ВОВ. Я очень хотела бы, чтобы вы об этом вспомнили и не забыли поздравить ветеранов, живущих рядом с вами..

Актуализация опорных знаний

Чтобы успешно справиться со следующим заданием давайте напомним алгоритм решения квадратных уравнений. (Фронтальный опрос)

Памятка для решения дробных рациональных уравнений

Алгоритм решения дробных рациональных уравнений

Найти общий знаменатель дробей, входящих в уравнение.

Задать ОДЗ (область допустимых значений). Для этого приравнять знаменатель к нулю и решить полученное уравнение.

Умножить обе части уравнения на общий знаменатель.

Найти дополнительные множители к дробям.

Решить получившееся целое уравнение.

Исключить из корней те, которые обращают общий знаменатель в нуль.

В. Для вычисления квадратов чисел от 10 до 99 какой таблицей будем пользоваться?

О. Таблицей квадратов натуральных чисел, которая находится на форзаце учебника

Работа в группах

У вас на столе находятся карточки с заданиями разных уровней: красный цвет – 5; зеленый – 4; желтый – 3. Вы выбираете сами себе уравнение. Решаете его самостоятельно. Можно в группе решить уравнение и другого уровня. Итог этой работы заключается в следующем: группой решить все уравнения и по ответам собрать свою мозаику. Приклеить ее на лист. Т.к. вы работаете в группах, то друг другу помогаете и по ответам, полученным при решении уравнений вы должны собрать мозаику, где обозначены пейзажи нашего поселка.

Карточка 1 (красная)

=

=

Карточка 2 (зеленая)

а)
=

=

б)
=

=

Карточка 3 (желтая)

а)
=

=
Учащиеся подсчитывают количество баллов и поставьте оценку в оценочный лист. Эти листы сдается учителю.

Оценка «5» - от 8 баллов и выше

Оценка «4» - 7 баллов

Оценка «3» - 4 – 6 баллов

Урок подходит к концу. Спасибо огромное за работу. Мне было легко работать с вами. А что вы можете сказать об уроке, о вашем состоянии на уроке? Прошу найти на столе карточки с рефлексией и назвать одним предложением ваше настроение. Достигли ли мы целей урока, все ли было понятно, и т.д. (по 1 ученику от группы)

Рефлексия

Я успеваю улыбнуться

Сколько слов и надежд

Давайте горевать и плакать откровенно

Ой, как хорошо, хоть песни пой

Доволен я своей судьбой

Неприятность эту мы переживём

Ах, зачем же этот день кончается

Не надо зла таить

Всё пока ещё в полном порядке

Кап-кап-кап из глаз на платье

Оценочный лист

Ф.И.

Проверка домашнего задания

Фронтальный опрос

Работа по карточкам

Итог урока