Выражения, преобразование выражений

Как освободиться от иррациональности в знаменателе? Способы, примеры, решения

В 8 классе на уроках алгебры в рамках темы преобразование иррациональных выражений заходит разговор про освобождение от иррациональности в знаменателе дроби . В этой статье мы разберем, что это за преобразование, рассмотрим, какие действия позволяют освободиться от иррациональности в знаменателе дроби, и приведем решения характерных примеров с детальными пояснениями.

Навигация по странице.

Что значит освободиться от иррациональности в знаменателе дроби?

Сначала нужно разобраться, что такое иррациональность в знаменателе и что значит освободиться от иррациональности в знаменателе дроби. В этом нам поможет информация из школьных учебников . Заслуживают внимания следующие моменты.

Когда запись дроби содержит в знаменателе знак корня (радикал), то говорят, что в знаменателе присутствует иррациональность . Вероятно, это связано с тем, что записанные при помощи знаков корней числа часто являются . В качестве примера приведем дроби , , , , очевидно, знаменатели каждой из них содержат знак корня, а значит и иррациональность. В старших классах неизбежна встреча с дробями, иррациональность в знаменатели которых вносят не только знаки квадратных корней, но и знаки кубических корней, корней четвертой степени и т.д. Вот примеры таких дробей: , .

Учитывая приведенную информацию и смысл слова «освободиться», очень естественно воспринимается следующее определение:

Определение.

Освобождение от иррациональности в знаменателе дроби – это преобразование, при котором дробь с иррациональностью в знаменателе заменяется тождественно равной дробью, не содержащей в знаменателе знаков корней.

Часто можно слышать, что говорят не освободиться, а избавиться от иррациональности в знаменателе дроби. Смысл при этом не меняется.

Например, если от дроби перейти к дроби , значение которой равно значению исходной дроби и знаменатель которой не содержит знака корня, то можно констатировать, что мы освободились от иррациональности в знаменателе дроби. Еще пример: замена дроби тождественно равной ей дробью есть освобождение от иррациональности в знаменателе дроби.

Итак, начальная информация получена. Остается узнать, что нужно делать, чтобы освободиться от иррациональности в знаменателе дроби.

Способы освобождения от иррациональности, примеры

Обычно для освобождения от иррациональности в знаменателе дроби используют два преобразования дроби : умножение числителя и знаменателя на отличное от нуля число или выражение и преобразование выражения в знаменателе. Ниже мы рассмотрим, как эти преобразования дробей используются в рамках основных способов, позволяющих избавиться от иррациональности в знаменателе дроби. Затронем следующие случаи.

В самых простых случаях достаточно преобразовать выражение в знаменателе. В качестве примера можно привести дробь, в знаменателе которой находится корень из девяти. В этом случае замена его значением 3 освобождает знаменатель от иррациональности.

В более сложных случаях приходится предварительно выполнять умножение числителя и знаменателя дроби на некоторое отличное от нуля число или выражение, что впоследствии позволяет преобразовать знаменатель дроби к виду, не содержащему знаков корней. Например, после умножения числителя и знаменателя дроби на , дробь принимает вид , а дальше выражение в знаменателе можно заменить выражением без знаков корней x+1 . Таким образом, после освобождения от иррациональности в знаменателе дробь принимает вид .

Если говорить про общий случай, то чтобы избавиться от иррациональности в знаменателе дроби, приходится прибегать к различным допустимым преобразованиям, иногда, довольно специфическим.

А теперь подробно.

Преобразование выражения в знаменателе дроби

Как уже было отмечено, один из способов избавления от иррациональности в знаменателе дроби состоит в преобразовании знаменателя. Рассмотрим решения примеров.

Пример.

Избавиться от иррациональности в знаменателе дроби .

Решение.

Раскрыв скобки в знаменателе, придем к выражению . Дальше позволяют перейти к дроби . Вычислив значения под знаками корней, имеем . Очевидно, в полученном выражении можно , что дает дробь , которая равна 1/16 . Так мы избавились от иррациональности в знаменателе.

Обычно решение записывают кратко без пояснения, так как выполняемые действия довольно просты:

Ответ:

.

Пример.

Решение.

Когда мы говорили про преобразование иррациональных выражений с использованием свойств корней , то отметили, что для любого выражения A при четных n (в нашем случае n=2 ) выражение можно заменить выражением |A| на всей ОДЗ переменных для исходного выражения. Поэтому, можно выполнить такое преобразование заданной дроби: , которое освобождает от иррациональности в знаменателе.

Ответ:

.

Умножение числителя и знаменателя на корень

Когда выражение в знаменателе дроби имеет вид , где выражение A не содержит знаков корней, то освободиться от иррациональности в знаменателе позволяет умножение числителя и знаменателя на . Это действие возможно, так как не обращается в нуль на ОДЗ переменных для исходного выражения. При этом в знаменателе получается выражение , которое легко преобразовать к виду без знаков корней: . Покажем применение этого подхода на примерах.

Пример.

Освободитесь от иррациональности в знаменателе дроби: а) , б) .

Решение.

а) Умножив числитель и знаменатель дроби на квадратный корень из трех, получим .

б) Чтобы избавиться от знака квадратного корня в знаменателе, умножим числитель и знаменатель дроби на , после чего проведем преобразования в знаменателе:

Ответ:

а) , б) .

В случае, когда в знаменателе находятся множители или , где m и n некоторые натуральные числа, числитель и знаменатель надо умножить на такой множитель, чтобы после этого выражение в знаменателе можно было преобразовать к виду или , где k – некоторое натуральное число, соответственно. Дальше легко перейти к дроби без иррациональности в знаменателе. Покажем применение описанного способа избавления от иррациональности в знаменателе на примерах.

Пример.

Освободиться от иррациональности в знаменателе дроби: а) , б) .

Решение.

а) Ближайшее натуральное число, превосходящее 3 и делящееся на 5 , есть 5 . Чтобы показатель шестерки стал равен пяти, выражение в знаменателе надо умножить на . Следовательно, освобождению от иррациональности в знаменателе дроби будет способствовать выражение , на которое надо умножить числитель и знаменатель:

б) Очевидно, что ближайшее натуральное число, которое превосходит 15 и при этом делится без остатка на 4 , это 16 . Чтобы получить показатель степени в знаменателе стал равен 16 , нужно умножить находящееся там выражение на . Таким образом, умножение числителя и знаменателя исходной дроби на (заметим, значение этого выражения не равно нулю при при каких действительных x ) позволит избавиться от иррациональности в знаменателе:

Ответ:

а) , б) .

Умножение на сопряженное выражение

Следующий способ освобождения от иррациональности в знаменателе дроби покрывает случаи, когда в знаменателе находятся выражения вида , , , , или . В этих случаях, чтобы освободиться от иррациональности в знаменателе дроби, надо числитель и знаменатель дроби умножить на так называемое сопряженное выражение .

Осталось узнать, какие выражения являются сопряженными для указанных выше. Для выражения сопряженным выражением является , а для выражения сопряженным является выражение . Аналогично, для выражения сопряженным является , а для выражения сопряженным является . И для выражения сопряженным является , а для выражения сопряженным является . Итак, выражение, сопряженное данному выражению, отличается от него знаком перед вторым слагаемым.

Давайте посмотрим, к чему приводит умножение выражения на сопряженное ему выражение. Для примера рассмотрим произведение . Его можно заменить разностью квадратов, то есть, , откуда дальше можно перейти к выражению a−b , которое не содержит знаков корней.

Теперь становится понятно, как умножение числителя и знаменателя дроби на выражение, сопряженное знаменателю, позволяет освободиться от иррациональности в знаменателе дроби. Рассмотрим решения характерных примеров.

Пример.

Представьте выражение в виде дроби, знаменатель которой не содержит радикала: а) , б) .

Решение.

а) Выражение, сопряженное знаменателю, это . Умножим на него числитель и знаменатель, что позволит нам освободиться от иррациональности в знаменателе дроби:

б) Для выражения сопряженным является . Умножая на него числитель и знаменатель, получаем

Можно было сначала вынести знак минус из знаменателя, а уже после этого умножать числитель и знаменатель на выражение, сопряженное знаменателю:

Ответ:

а) , б) .

Обратите внимание: при умножении числителя и знаменателя дроби на выражение с переменными, сопряженное знаменателю, нужно позаботиться, чтобы оно не обращалось в нуль ни при каком наборе значений переменных из ОДЗ для исходного выражения.

Пример.

Освободиться от иррациональности в знаменателе дроби .

Решение.

Для начала найдем область допустимых значений (ОДЗ) переменной x . Она определяется условиями x≥0 и , из которых заключаем, что ОДЗ есть множество x≥0 .

Выражение, сопряженное знаменателю, есть . Мы можем умножить на него числитель и знаменатель дроби при условии, что , которое на ОДЗ равносильно условию x≠16 . При этом имеем

А при x=16 имеем .

Таким образом, для всех значений переменной x из ОДЗ, кроме x=16 , , а при x=16 имеем .

Ответ:

Использование формул сумма кубов и разность кубов

Из предыдущего пункта мы узнали, что умножение числителя и знаменателя дроби на выражение, сопряженное знаменателю, проводится для того, чтобы в дальнейшем применить формулу разность квадратов и тем самым освободиться от иррациональности в знаменателе. В некоторых случаях для освобождения от иррациональности в знаменателе оказываются полезными и другие формулы сокращенного умножения . Например, формула разность кубов a 3 −b 3 =(a−b)·(a 2 +a·b+b 2) позволяет избавиться от иррациональности, когда в знаменателе дроби находятся выражения с кубическими корнями вида или , где A и B – некоторые числа или выражения. Для этого числитель и знаменатель дроби умножается на неполный квадрат суммы или на разность соответственно. Аналогично примеряется и формула сумма кубов a 3 +b 3 =(a+b)·(a 2 −a·b+b 2) .

Пример.

Освободитесь от иррациональности в знаменателе дроби: а) , б) .

Решение.

а) Несложно догадаться, что в данном случае освободиться от иррациональности в знаменателе позволяет умножение числителя и знаменателя на неполный квадрат суммы чисел и , так как в дальнейшем это позволит преобразовать выражение в знаменателе по формуле разность кубов:

б) Выражение в знаменателе дроби можно представить в виде , из которого хорошо видно, что это неполный квадрат разности чисел 2 и . Таким образом, если числитель и знаменатель дроби умножить на сумму , то знаменатель можно будет преобразовать по формуле сумма кубов, что позволит освободиться от иррациональности в знаменателе дроби. Это возможно сделать при условии , которое равносильно условию и дальше x≠−8 :

А при подстановке x=−8 в исходную дробь имеем .

Таким образом, для всех x из ОДЗ для исходной дроби (в данном случае это множество R ), кроме x=−8 , имеем , а при x=8 имеем .

Ответ:

Использование различных способов

В примерах посложнее обычно не получается в одно действие освободиться от иррациональности в знаменателе, а приходится последовательно применять метод за методом, в том числе и из разобранных выше. Иногда могут потребоваться и какие-нибудь нестандартные приемы решения. Довольно интересные задания по обсуждаемой теме можно найти в учебнике под авторством Колягина Ю. Н. Список литературы.

1. Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 16-е изд. - М. : Просвещение, 2008. - 271 с. : ил. - ISBN 978-5-09-019243-9.
2. Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. - 11-е изд., стер. - М.: Мнемозина, 2009. - 215 с.: ил. ISBN 978-5-346-01155-2.
3. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М. И. Шабунин]; под ред. А. Б. Жижченко. - 3-е изд. - М. : Просвещение, 2010.- 368 с. : ил.- ISBN 978-5-09-022771-1.

Рассмотрим задачу из алгебры многочленов.

Задача 4.1

Пусть а является корнем многочлена х 3 + 6х - 3. Нужно освободиться от алгебраической иррациональности в знаменателе дроби

Т.е. представить дробь в виде многочлена от а с рацио-

нальными коэффициентами.

Решение. Знаменатель дроби есть значение от а многочлена fix) =х 2 + 5, а минимальным многочленом алгебраического элемента а является ф(х) =х 3 + 6х- 3, поскольку этот многочлен неприводим над полем Q (по критерию Эйзенштейна при простом р = 3). Найдем НОДОс 3 + 6х - 3, х 2 + 5) с помощью алгоритма Евклида:

Обобщим ситуацию и рассмотрим общую задачу.

Задача об освобождении от алгебраической иррациональности в знаменателе дроби

Пусть а - алгебраическая иррациональность над полем Р с ми-

, . „ а к а к +a k _,a k ~ l -f-. + aia + Oo

нимальным многочленом фОО и В = - - 1

Ъ т а т + bro-ioc" 1 - 1 +... + bja + b 0

где коэффициенты многочленов в числителе и знаменателе дроби принадлежат полю Р. Освободиться от алгебраической иррациональности в знаменателе дроби, т.е. представить (3 в виде

где коэффициенты принадлежат полю Р.

Решение. Обозначим/)*) = b nl x" + b m _ 1 x nl_1 +... + b } x + b 0 и у =/(а). Поскольку у ^ 0, то по свойству минимального многочлена НОД(/(х), ф(х)) = 1. Используя алгоритм Евклида, находим многочлены u(x) и v(x), такие что f(x) и (х) + ф(х)у(х) = 1. Отсюда Да) и (а) + ф(а)у(а) = 1, а так как ф(а) = 0, тоДа)и(а) = 1. Следовательно, умножая числитель и знаменатель данной дроби на ц(а), в знаменателе получим единицу, и задача решена.

Заметим, что общий прием освобождения от алгебраической иррациональности в знаменателе дроби в случае комплексных а + Ы

чисел-приводит к известной процедуре умножения числи-

теля и знаменателя на число, сопряженное знаменателю.

Исторический экскурс

Впервые существование чисел, трансцендентных над полем Q, обнаружил Ж. Лиувилль (1809-1882) в работах 1844 и 1851 гг. Одним из трансцендентных чисел Лиувилля является число

Ш. Эрмит (1822-

а= У--. Вдесятичнойзаписиа = 0Д100010..

кл 10*

1901) доказал трансцендентность числа е в 1873 г., а К. Ф. Линде- ман (1852-1939) доказал в 1882 г. трансцендентность числа п. Эти результаты были получены очень не просто. В то же время совсем просто Г. Кантор (1845-1918) доказал, что трансцендентных чисел «значительно больше», чем алгебраических: трансцендентных чисел «столько же», сколько всех действительных чисел, в то время как алгебраических чисел «столько же», сколько всех натуральных чисел. Точнее, множество алгебраических чисел счетно, а множество трансцендентных чисел несчетно. Доказательство этого факта, устанавливая существование трансцендентных чисел, не дает рецепта получения ни одного из них. Такого рода теоремы существования чрезвычайно важны в математике уже тем, что вселяют веру в успех поиска объекта, существование которого доказано. Вместе с тем существует направление в математике, представители которого не признают чистых теорем существования, называя их неконструктивными. Наиболее яркими из этих представителей являются Л. Кронекер и Я. Брауэр.

В 1900 г. на Всемирном конгрессе математиков в Париже немецкий математик Д. Гильберт (1862-1943) сформулировал следующую проблему 22: Какова природа числа аР, где а и (3 - алгебраические числа, а ^ 0, а ^ 1 и степень алгебраического числа (3 не меньше 2? А. О. Гельфонд (1906-1968) доказал, что такие числа трансцендентны. Отсюда следует, в частности, что числа 2^, З г являются трансцендентными.

При преобразовании дробного алгебраического выражения, в знаменателе которого записано иррациональное выражение, обычно стремятся представить дробь так, чтобы ее знаменатель был рациональным. Если A,B,C,D,... - некоторые алгебраические выражения, то можно указать правила, с помощью которых можно освободиться от знаков радикала в знаменателе выражений вида

Во всех этих случаях освобождение от иррациональности производится умножением числителя и знаменателя дроби на множитель, выбранный так, чтобы его произведение на знаменатель дроби было рациональным.

1) Для освобождения от иррациональности в знаменателе дроби вида . В умножаем числитель и знаменатель на

Пример 1. .

2) В случае дробей вида . Умножаем числитель и знаменатель на иррациональный множитель

соответственно, т. е. на сопряженное иррациональное выражение.

Смысл последнего действия состоит в том, что в знаменателе произведение суммы на разность преобразуется в разность квадратов, которая уже будет рациональным выражением.

Пример 2. Освободиться от иррациональности в знаменателе выражения:

Решение, а) Умножаем числитель и знаменатель дроби на выражение . Получаем (при условии, что )

3) В случае выражений типа

знаменатель рассматривается как сумма (разность) и умножается на неполный квадрат разности (суммы), чтобы получить сумму (разность) кубов ((20.11), (20.12)). На тот же множитель умножается и числитель.

Пример 3. Освободиться от иррациональности в знаменателе выражений:

Решение, а) Рассматривая знаменатель данной дроби как сумму чисел и 1, умножим числитель и знаменатель на неполный квадрат разности этих чисел:

или окончательно:

В некоторых случаях требуется выполнить преобразование противоположного характера: освободить дробь от иррациональности в числителе. Оно проводится совершенно аналогично.

Пример 4. Освободиться от иррациональности в числителе дроби .

Урок №1 Тема урока: «Освобождение от иррациональности в знаменателе дроби»

Цели:

Образовательная:

Развивающая:

Воспитательная: воспитание последовательности в своих действиях.

Тип урока: изучение нового

Стандарт урока:

уметь находить способ избавления от иррациональности

понимать смысл «сопряженное выражение»

уметь избавляться от иррациональности в знаменателе.

Оборудование: карточки к самостоятельной работе.

Ход урока

Извлекать корни умеешь? – спрашивает учитель

Да, конечно. Нужно потянуть за стебель растения посильнее, и корень его извлечётся из почвы.

Нет, я имел в виду другой корень, например, из девяти.

Это будет «девя», так как «ть»-суффикс.

Я имею в виду корень квадратный.

Квадратных корней не бывает. Они бывают мочковатые и стержневые.

Арифметический квадратный корень из девяти.

Так бы и сказали! Квадратный корень из девяти =3!

А вы корни извлекать умеете?

2. «Повторение – мать учения».

(8 мин)

2.Проверка дом/з № 168 1)4; 2)10; 3)4;4) 8

3.Разминка. Выполни действия (Слайд 1). Проверка по кругу против часовой стрелки.

1. Подбери неизвестный множитель (Слайд2)

Деление на группы: по выбранным фигурам.

Проверяют в парах сменного состава.

Работают индивидуально и проверяют, оценивая в баллах.

(Приложение 1)

3. «Книга – книгой, а мозгами двигай» (5 мин)

(Слайд 3) Два друга решали уравнение
и получили разные ответы. Один из них подобрал х = , сделал проверку. Второй находил неизвестный множитель делением произведения на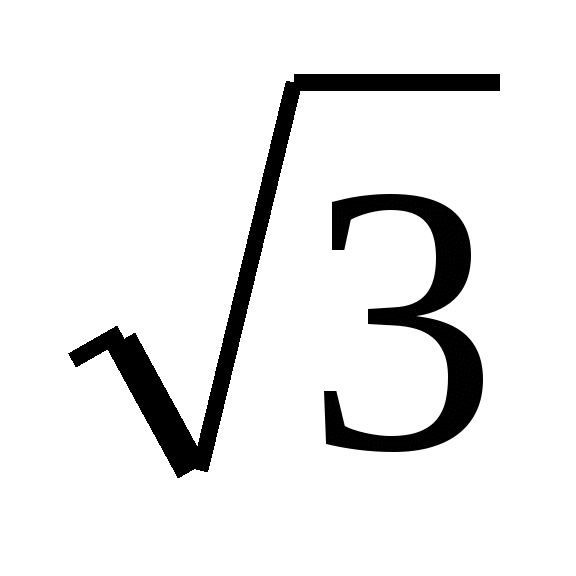
и получил х = . Кто из них прав? Может ли линейное уравнение иметь два корня? Самым удобным для вычислений является выражение, не содержащее иррациональности в знаменателе.

Тема урока (Слайд 4): Освобождение от иррациональности в знаменателе дроби

Цели (Слайд 5): ознакомиться со способами избавления от иррациональности в знаменатели дроби. Развитие умения освобождать знаменатель от иррациональности;

Решают и проверяют в парах сменного состава.

Обсуждают ситуацию и приходят к выводу.

Записывают тему

Формулируют цели : ознакомиться со способами избавления от иррациональности в знаменатели дроби.

развитие умения определять способ освобождения от иррациональности;

4. Работа над новым материалом.

(10 мин)

Как избавиться от иррациональности в знаменателе? Хотите узнать?

Работа в группах над новым материалом

Выступление групп

Закрепление (Слайд 6)

Работают с опорным конспектом. (Приложение 2)

Решают примеры.

(Приложение 3)

Обмениваются информацией.

5. Зарядка (3 мин)

Делают зарядку

6. Самостоятельная работа

(10 мин)

По разноуровневым карточкам

1-в:

2-в:

3-в:

Выполняют индивидуально, проверяют меняясь тетрадями с другой группой.

Баллы заносят в оценочную карту группы.

(Приложение 1)

7.Творческое задание

(2 мин)

Мартышка – апельсинов продавщица,(Слайд 7)

Приехав как – то раз к себе на дачу,

Нашла там с радикалами задачу.

Разбрасывать их стала все подряд.

Мы просим вас, девчонки и мальчишки,

Решить задачу на хвосте мартышки.

Как вы думаете мы закончили изучать эту тему? Продолжим на следующем уроке.

Рассуждают о том, что это им предстоит узнать на следующем уроке.

8. Задание на дом: (2 мин)

П.19(Слайд 7)

1 уровень: №170 (1-6)

2 уровень: №170 (1-6 и 9,12)

Творческое задание: Мартышкина задача.

Записывают

9.Итог урока. Рефлексия

(3 мин)

Две звезды и пожелание на стикерах прикрепляются на выбранный смайлик (Слайд 7)

Баллы переводят в оценку и сдают учителю оценочную карту группы.

ПРИЛОЖЕНИЕ 1

Оценочная карта группы.

0-8 баллов

Подбери множитель

0-8 баллов

Работа в группе над новым материалом

0-5 баллов

Сам. работа

0-5 баллов

Активность на уроке

0-5 баллов

ПРИЛОЖЕНИЕ 2

Опорный конспект

Если знаменатель алгебраической дроби содержит знак квадратного корня, то говорят, что в знаменателе содержится иррациональность. Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют освобождением от иррациональности в знаменателе

Преобразование выражений, содержащих арифметические квадратные корни

Цель урока: создание условий для формирования умений, упрощать выражения, содержащие арифметические квадратные корни в ходе работы в группах сменного состава.

Задачи урока: проверить теоретическую подготовку учащихся, умение извлекать квадратный корень из числа, формировать навыки правильного воспроизведения своих знаний и умений, развивать вычислительные навыки, воспитывать умение работать в парах и ответственности за общее дело.

Ход урока.

I . Организационный момент. « ТАБЛИЦА ГОТОВНОСТИ»

Фиксация уровня готовности к началу занятия.

25 карточек красного цвета (5 баллов), желтого цвета (4 балла), синего

цвета (3 балла).

Таблица готовности

5 баллов (хочу знать, делать, решать)

4 балла (я готов к работе)

3 балла (я не очень хорошо себя чувствую, я не понимаю материал, мне нужна помощь)

II . Индивидуальная работа по карточкам

Карточка 1

Вынести множитель из-под знака корня:

Карточка 2

Внести множитель под знак корня:

Карточка 3

Упростить:
а)
б)
в)

(Проверка после проверки домашнего задания)

III . Проверка домашнего задания.

№166, 167 устно фронтально

(самооценивание с помощью сигнальных карточек: зелёный - всё верно, красный – есть ошибка)

IV . Изучение нового материала. Работа в группах сменного состава.

Самостоятельно изучить материал, чтобы потом суметь объяснить его членам группы. Класс делится на 6 групп по 4 человека.

1, 2 и 3 группы – учащиеся со средними способностями

Как избавиться от иррациональности в знаменателе дроби? Рассмотрим общий случай и конкретные примеры.

Если число или выражение, стоящее под знаком квадратного корня в знаменателе, является одним из множителей, чтобы избавиться от иррациональности в знаменателе и числитель, и знаменатель дроби умножаем на квадратный корень из этого числа или выражения:

Примеры.

1) ;

2) .

4, 5 и 6 группы – учащиеся со способностями выше средних.

Если знаменатель дроби - сумма либо разность двух выражений, содержащих квадратный корень, чтобы избавиться от иррациональности в знаменателе умножаем и числитель, и знаменатель на сопряженный радикал:

Примеры. Освободиться от иррациональности в знаменателе дроби:

Работа в новых группах (4 группы по 6 человек, от каждой группы по 1 человеку).

Объяснение изученного материала членам новой группы. (взаимооценивание – прокомментировать объяснение материала учеником)

V . Проверка усвоения теоретического материала. На вопросы отвечают учащиеся, не объясняющие данную часть теоретического материала.

1) Как избавиться от иррациональности в знаменателе дроби, если число или выражение, стоящее под знаком квадратного корня в знаменателе, является одним из множителей?

2) Как избавиться от иррациональности в знаменателе дроби, если знаменатель дроби - сумма либо разность двух выражений, содержащих квадратный корень?

3) как избавиться от иррациональности в знаменателе дроби

4) Как избавиться от иррациональности в знаменателе дроби

VI . Закрепление изученного материала. Проверочная самостоятельная работа.

№81 («Алгебра» 8 класс, А.Абылкасымова, И.Бекбоев, А.Абдиев, З,Жумагулова)

№170 (1,2,3,5,6) («Алгебра» 8 класс, А.Шыныбеков)

Критерии оценивания:

Уровень А – № 81 примеры 1-5 отметка «3»

Уровень В – № 81 примеры 6-8 и №170 примеры 5,6 отметка «4»

Уровень С – № 170 примеры 1-6 отметка «5»

(самооценивание, проверка по образцу в флипчарте)

VII . Домашнее задание.

№ 218

VIII . Рефлексия. « Телеграмма»

Каждому предлагается заполнить бланк телеграммы, получив при этом следующую инструкцию: «Что вы думаете о прошедшем занятии? Что было для вас важным? Чему вы научились? Что вам понравилось? Что осталось неясным? В каком направлении нам стоит продвигаться дальше? Напишите мне, пожалуйста, об этом короткое послание –телеграмму из 11 слов. Я хочу узнать ваше мнение для того, чтобы учитывать его в дальнейшей работе».

Итог урока.