Как решать тригонометрические уравнения на промежутке. Решение тригонометрических уравнений и способы отбора корней на заданном промежутке
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| \leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`

Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`

4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`

Формулы корней тригонометрических уравнений в таблице
Для синуса: Для косинуса:
Для косинуса: Для тангенса и котангенса:
Для тангенса и котангенса: Формулы решения уравнений, содержащих обратные тригонометрические функции:
Формулы решения уравнений, содержащих обратные тригонометрические функции:

Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 — x)+1=0`
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
делаем замену: `cos(x+\frac \pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Ответ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя , преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n`, `x_2=\pi/2+ 2\pi n`.
Ответ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x \ne 0` — для первого случая, и на `cos^2 x \ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x \ne 0`, получим:
`\frac {sin^2 x}{cos^2 x}+\frac{sin x cos x}{cos^2 x} — \frac{2 cos^2 x}{cos^2 x}=0`
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Ответ. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Ответ. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt {a^2+b^2}`:
`\frac a{sqrt {a^2+b^2}} sin x +` `\frac b{sqrt {a^2+b^2}} cos x =` `\frac c{sqrt {a^2+b^2}}`.
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `\frac a{sqrt {a^2+b^2}}=cos \varphi`, ` \frac b{sqrt {a^2+b^2}} =sin \varphi`, `\frac c{sqrt {a^2+b^2}}=C`, тогда:
`cos \varphi sin x + sin \varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt {3^2+4^2}`, получим:
`\frac {3 sin x} {sqrt {3^2+4^2}}+` `\frac{4 cos x}{sqrt {3^2+4^2}}=` `\frac 2{sqrt {3^2+4^2}}`
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos \varphi` , `4/5=sin \varphi`. Так как `sin \varphi>0`, `cos \varphi>0`, то в качестве вспомогательного угла возьмем `\varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos \varphi sin x+sin \varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`sin (x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `\frac {sin x}{1+cos x}=1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
`\frac {sin x}{1+cos x}=` `\frac {(1-cos x)(1+cos x)}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {1-cos^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {sin^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}-` `\frac {sin^2 x}{1+cos x}=0`
`\frac {sin x-sin^2 x}{1+cos x}=0`
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Цель урока:
а) закрепить умения решать простейшие тригонометрические уравнения ;
б) научить выбирать корни тригонометрических уравнений из заданного промежутка
Ход урока.
1. Актуализация знаний.
а)Проверка домашнего задания: классу дано опережающее домашнее задание – решить уравнение и найти способ выбора корней из данного промежутка.
1)cos x = -0,5, где хI [- ]. Ответ: .
2) sin x = , где хI . Ответ: ; .
3)cos 2x = -, где хI . Ответ:
Ученики записывают решение на доске кто-то с помощью графика, кто-то методом подбора.
В это время класс работает устно.
Найдите значение выражения:
а) tg – sin + cos + sin . Ответ: 1.
б) 2arccos 0 + 3 arccos 1. Ответ: ?
в) arcsin + arcsin . Ответ: .
г) 5 arctg (-) – arccos (-). Ответ:– .
– Проверим домашнее задание, откройте свои тетради с домашними работами.
Некоторые из вас нашли решение методом подбора, а некоторые с помощью графика.
2. Вывод о способах решения данных заданий и постановка проблемы, т. е. сообщение темы и цели урока.
– а) С помощью подбора решать сложно, если задан большой промежуток.
– б) Графический способ не даёт точных результатов, требует проверку, и занимает много времени.
– Поэтому должен быть ещё как минимум один способ, наиболее универсальный -попробуем его найти. Итак, чем мы будем заниматься сегодня на уроке? (Учиться выбирать корни тригонометрического уравнения на заданном промежутке.)
– Пример 1. (Ученик выходит к доске)
cos x = -0,5, где хI [- ].
Вопрос: Отчего зависит ответ на данное задание? (От общего решения уравнения. Запишем решение в общем виде). Решение записывается на доске
х = + 2?k, где k R.
– Запишем это решение в виде совокупности:

– Как вы считаете, при какой записи решения удобно выбирать корни на промежутке? (из второй записи). Но это ведь опять способ подбора. Что нам необходимо знать, чтобы получить верный ответ? (Надо знать значения k).
(Составим математическую модель для нахождения k).
так как kI Z, то k = 0, отсюда х = = |
из данного неравенства видно, что целочисленныхзначений k нет. |
Вывод: Чтобы выбрать корни из заданного промежутка при решении тригонометрического уравнения надо:
- для решения уравнения вида sin x = a , cos x = a удобнее записать корни уравнения, как две серии корней.
- для решения уравнений вида tg x = a , ctg x = a записать общую формулу корней.
- составить математическую модель для каждого решения в виде двойного неравенства и найти целое значение параметра k или n.
- подставить эти значения в формулу корней и вычислить их.
Пример №2 и №3 из домашнего задания решить, используя полученный алгоритм. Одновременно у доски работают два ученика, с последующей проверкой работ.
Обязательный минимум знаний
sin x = a, -1 a 1 (a 1)x = arcsin a + 2 n, n Z
x = - arcsin a + 2 n, n Z
или
x = (- 1)k arcsin a + k, k Z
arcsin (- a) = - arcsin a
sin x = 1
x = /2 + 2 k, k Z
sin x = 0
x = k, k Z
sin x = - 1
x = - /2 + 2 k, k Z
y
y
x
y
x
x
Обязательный минимум знаний
cos x = a, -1 a 1 (a 1)x = arccos a + 2 n, n Z
arccos (- a) = - arccos a
cos x = 1
x = 2 k, k Z
cos x = 0
x = /2 + k, k Z
y
y
x
cos x = - 1
x = + 2 k, k Z
y
x
x
Обязательный минимум знаний
tg x = a, a Rx = arctg a + n, n Z
ctg x = a, a R
x = arcctg a + n, n Z
arctg (- a) = - arctg a
arctg (- a) = - arctg a Свести уравнение к одной функции
Свести к одному аргументу
Некоторые методы решения
тригонометрических уравнений
Применение тригонометрических формул
Использование формул сокращённого умножения
Разложение на множители
Сведение к квадратному уравнению относительно sin x, cos x, tg x
Введением вспомогательного аргумента
Делением обеих частей однородного уравнения первой степени
(asin x +bcosx = 0) на cos x
Делением обеих частей однородного уравнения второй степени
(a sin2 x +bsin x cos x+ c cos2x =0) на cos2 x
Устные упражнения Вычислите
arcsin ½arcsin (- √2/2)
arccos √3/2
arccos (-1/2)
arctg √3
arctg (-√3/3)
= /6
= - /4
= /6
= - arccos ½ = - /3 = 2 /3
= /3
= - /6
(с помощью тригонометрической окружности)
cos 2x = ½, x [- /2; 3 /2]
2x = ± arccos ½ + 2 n, n Z
2x = ± /3 + 2 n, n Z
x = ± /6 + n, n Z
Отберём корни с помощью тригонометрической окружности
Ответ: - /6; /6; 5 /6; 7 /6
Различные способы отбора корней
Найти корни уравнения, принадлежащие данному промежуткуsin 3x = √3/2, x [- /2; /2]
3x = (– 1)k /3 + k, k Z
x = (– 1)k /9 + k/3, k Z
Отберём корни с помощью перебора значений k:
k = 0, x = /9 – принадлежит промежутку
k = 1, x = – /9 + /3 = 2 /9 – принадлежит промежутку
k = 2, x = /9 + 2 /3 = 7 /9 – не принадлежит промежутку
k = – 1, x = – /9 – /3 = – 4 /9 – принадлежит промежутку
k = – 2, x = /9 – 2 /3 = – 5 /9 – не принадлежит промежутку
Ответ: -4 /9; /9; 2 /9
Различные способы отбора корней
Найти корни уравнения, принадлежащие данному промежутку(с помощью неравенства)
tg 3x = – 1, x (- /2;)
3x = – /4 + n, n Z
x = – /12 + n/3, n Z
Отберём корни с помощью неравенства:
– /2 < – /12 + n/3 < ,
– 1/2 < – 1/12 + n/3 < 1,
– 1/2 + 1/12 < n/3 < 1+ 1/12,
– 5/12 < n/3 < 13/12,
– 5/4 < n < 13/4, n Z,
n = – 1; 0; 1; 2; 3
n = – 1, x = – /12 – /3 = – 5 /12
n = 0, x = – /12
n = 1, x = – /12 + /3 = /4
n = 2, x = – /12 + 2 /3 = 7 /12
n = 3, x = – /12 + = 11 /12
Ответ: – 5 /12; – /12; /4; 7 /12; 11 /12
10. Различные способы отбора корней
Найти корни уравнения, принадлежащие данному промежутку(с помощью графика)
cos x = – √2/2, x [–4; 5 /4]
x = arccos (– √2/2) + 2 n, n Z
x = 3 /4 + 2 n, n Z
Отберём корни с помощью графика:
x = – /2 – /4 = – 3 /4; x = – – /4 = – 5 /4
Ответ: 5 /4; 3 /4
11. 1. Решить уравнение 72cosx = 49sin2x и указать его корни на отрезке [; 5/2]
1. Решить уравнение 72cosx = 49sin2xи указать его корни на отрезке [ ; 5 /2]
Решим уравнение:
72cosx = 49sin2x,
72cosx = 72sin2x,
2cos x = 2sin 2x,
cos x – 2 sinx cosx = 0,
cos x (1 – 2sinx) = 0,
cos x = 0 ,
x = /2 + k, k Z
или
1 – 2sinx = 0,
sin x = ½,
x = (-1)n /6 + n, n Z
Проведём отбор корней с помощью
тригонометрической окружности:
x = 2 + /6 = 13 /6
Ответ:
а) /2 + k, k Z, (-1)n /6 + n, n Z
б) 3 /2; 5 /2; 13 /6
12. 2. Решить уравнение 4cos2 x + 8 cos (x – 3/2) +1 = 0 Найти его корни на отрезке
2. Решить уравнение 4cos2 x + 8 cos (x – 3 /2) +1 = 0Найти его корни на отрезке
4cos2 x + 8 cos (x – 3 /2) +1 = 0
4cos2x + 8 cos (3 /2 – x) +1 = 0,
4cos2x – 8 sin x +1 = 0,
4 – 4sin2 x – 8 sin x +1 = 0,
4sin 2x + 8sin x – 5 = 0,
D/4 = 16 + 20 = 36,
sin x = – 2,5
или
sin x = ½
x = (-1)k /6 + k, k Z
13. Проведем отбор корней на отрезке (с помощью графиков)
Проведем отбор корней на отрезке(с помощью графиков)
sin x = ½
Построим графики функций y = sin x и y = ½
x = 4 + /6 = 25 /6
Ответ: а) (-1)k /6 + k, k Z; б) 25 /6
14. 3. Решить уравнение Найти его корни на отрезке
4 – cos2 2x = 3 sin2 2x + 2 sin 4x4 (sin2 2x + cos2 2x) – cos2 2x = 3 sin2 2x + 4 sin 2x cos 2x,
sin2 2x + 3 cos2 2x – 4 sin 2x cos 2x = 0
Если cos2 2x = 0, то sin2 2x = 0, что невозможно, поэтому
cos2 2x 0 и обе части уравнения можно разделить на cos2 2x.
tg22x + 3 – 4 tg 2x = 0,
tg22x – 4 tg 2x + 3= 0,
tg 2x = 1,
2x = /4 + n, n Z
x = /8 + n/2, n Z
или
tg 2x = 3,
2x = arctg 3 + k, k Z
x = ½ arctg 3 + k/2, k Z
15.
4 – cos2 2x = 3 sin2 2x + 2 sin 4xx = /8 + n/2, n Z или x = ½ arctg 3 + k/2, k Z
Так как 0 < arctg 3< /2,
0 < ½ arctg 3< /4, то ½ arctg 3
является решением
Так как 0 < /8 < /4 < 1,значит /8
также является решением
Другие решения не попадут в
промежуток , так как они
получаются из чисел ½ arctg 3 и /8
прибавлением чисел, кратных /2.
Ответ: а) /8 + n/2, n Z ; ½ arctg 3 + k/2, k Z
б) /8; ½ arctg 3
16. 4. Решить уравнение log5(cos x – sin 2x + 25) = 2 Найти его корни на отрезке
4. Решить уравнение log5(cos x – sin 2x + 25) = 2Найти его корни на отрезке
Решим уравнение:
log5(cos x – sin 2x + 25) = 2
ОДЗ: cos x – sin 2x + 25 > 0,
cos x – sin 2x + 25 = 25, 25 > 0,
cos x – 2sin x cos x = 0,
cos x (1 – 2sin x) = 0,
cos x = 0,
x = /2 + n, n Z
или
1 – 2sinx = 0,
sin x = 1/2
x = (-1)k /6 + k, k Z
17.
Проведём отбор корней на отрезкеПроведём отбор корней на отрезке :
1) x = /2 + n, n Z
2 /2 + n 7 /2, n Z
2 1/2 + n 7/2, n Z
2 – ½ n 7/2 – ½, n Z
1,5 n 3, n Z
n = 2; 3
x = /2 + 2 = 5 /2
x = /2 + 3 = 7 /2
2) sin x = 1/2
x = 2 + /6 = 13 /6
x = 3 – /6 = 17 /6
Ответ: а) /2 + n, n Z ; (-1)k /6 + k, k Z
б) 13 /6 ; 5 /2; 7 /2; 17 /6
18. 5. Решить уравнение 1/sin2x + 1/sin x = 2 Найти его корни на отрезке [-5/2; -3/2]
5. Решить уравнение 1/sin2x + 1/sin x = 2Найти его корни на отрезке [-5 /2; -3 /2]
Решим уравнение:
1/sin2x + 1/sin x = 2
x k
Замена 1/sin x = t,
t2 + t = 2,
t2 + t – 2 = 0,
t1= – 2, t2 = 1
1/sin x = – 2,
sin x = – ½,
x = – /6 + 2 n, n Z
или
x = – 5 /6 + 2 n, n Z
1/sin x = 1,
sin x = 1,
x = /2 + 2 n, n Z
Исключается эта серия корней, т.к. -150º+ 360ºn выходит за пределы
заданного промежутка [-450º; -270º]
19.
Продолжим отбор корней на отрезкеРассмотрим остальные серии корней и проведём отбор корней
на отрезке [-5 /2; -3 /2] ([-450º; -270º]):
1) x = - /6 + 2 n, n Z
2) x = /2 + 2 n, n Z
-5 /2 - /6 + 2 n -3 /2, n Z
-5 /2 /2 + 2 n -3 /2, n Z
-5/2 -1/6 + 2n -3/2, n Z
-5/2 1/2 + 2n -3/2, n Z
-5/2 +1/6 2n -3/2 + 1/6, n Z
-5/2 - 1/2 2n -3/2 - 1/2, n Z
– 7/3 2n -4/3, n Z
– 3 2n -2, n Z
-7/6 n -2/3, n Z
-1,5 n -1, n Z
n = -1
n = -1
x = - /6 - 2 = -13 /6 (-390º)
x = /2 - 2 = -3 /2 (-270º)
Ответ: а) /2 + 2 n, n Z ; (-1)k+1 /6 + k, k Z
б) -13 /6 ; -3 /2
20. 6. Решить уравнение |sin x|/sin x + 2 = 2cos x Найти его корни на отрезке [-1; 8]
Решим уравнение|sin x|/sin x + 2 = 2cos x
1)Если sin x >0, то |sin x| =sin x
Уравнение примет вид:
2 cos x=3,
cos x =1,5 – не имеет корней
2) Если sin x <0, то |sin x| =-sin x
и уравнение примет вид
2cos x=1, cos x = 1/2,
x = ±π/3 +2πk, k Z
Учитывая, что sin x < 0, то
остаётся одна серия ответа
x = - π/3 +2πk, k Z
Произведём отбор корней на
отрезке [-1; 8]
k=0, x= - π/3 , - π < -3, - π/3 < -1,
-π/3 не принадлежит данному
отрезку
k=1, x = - π/3 +2π = 5π/3<8,
5 π/3 [-1; 8]
k=2, x= - π/3 + 4π = 11π/3 > 8,
11π/3 не принадлежит данному
отрезку.
Ответ: а) - π/3 +2πk, k Z
б) 5
π/3
21. 7. Решить уравнение 4sin3x=3cos(x- π/2) Найти его корни на промежутке
8. Решить уравнение √1-sin2x= sin xНайти его корни на промежутке
Решим уравнение √1-sin2x= sin x.
sin x ≥ 0,
1- sin2x = sin2x;
sin x ≥ 0,
2sin2x = 1;
sin x≥0,
sin x =√2/2; sin x = - √2/2;
sin x =√2/2
x=(-1)k /4 + k, k Z
sin x =√2/2
25. Проведём отбор корней на отрезке
Проведём отбор корней на отрезкеx=(-1)k /4 + k, k Z
sin x =√2/2
у =sin x и у=√2/2
5 /2 + /4 = 11 /4
Ответ: а) (-1)k /4 + k, k Z ;б) 11 /4
26. 9. Решить уравнение (sin2x + 2 sin2x)/√-cos x =0 Найти его корни на промежутке [-5; -7/2]
9. Решить уравнение (sin2x + 2 sin2x)/√-cos x =0Найти его корни на промежутке [-5 ; -7 /2]
Решим уравнение
(sin2x + 2 sin2x)/√-cos x =0.
1) ОДЗ: cos x <0 ,
/2 +2 n
2 sinx∙cos x + 2 sin2x =0,
sin x (cos x+ sin x) =0,
sin x=0, x= n, n Z
или
cos x+ sin х=0 | : cos x,
tg x= -1, x= - /4 + n, n Z
C учётом ОДЗ
x= n, n Z, x= +2 n, n Z;
x= - /4 + n, n Z,
x= 3 /4 + 2 n, n Z
27. Отберём корни на заданном отрезке
Отберём корни на заданномотрезке [-5 ; -7 /2]
x= +2 n, n Z ;
-5 ≤ +2 n ≤ -7 /2,
-5-1 ≤ 2n ≤ -7/2-1,
-3≤ n ≤ -9/4, n Z
n = -3, x= -6 = -5
x= 3 /4 + 2 n, n Z
-5 ≤ 3 /4 + 2 n ≤ -7 /2
-23/8 ≤ n ≤ -17/8, нет такого
целого n.
Ответ: а) +2 n, n Z ;
3 /4 + 2 n, n Z ;
б) -5 .
28. 10. Решить уравнение 2sin2x =4cos x –sinx+1 Найти его корни на промежутке [/2; 3/2]
10. Решить уравнение 2sin2x =4cos x –sinx+1Найти его корни на промежутке [ /2; 3 /2]
Решим уравнение
2sin2x = 4cos x – sinx+1
2sin2x = 4cos x – sinx+1,
4 sinx∙cos x – 4cos x + sin x -1 = 0,
4cos x(sin x – 1) + (sin x – 1) = 0,
(sin x – 1)(4cos x +1)=0,
sin x – 1= 0, sin x = 1, x = /2+2 n, n Z
или
4cos x +1= 0, cos x = -0,25
x = ± (-arccos (0,25)) + 2 n, n Z
Запишем корни этого уравнения иначе
x = - arccos(0,25) + 2 n,
x = -(- arccos(0,25)) + 2 n, n Z
29. Отберём корни с помощью окружности
x = /2+2 n, n Z, х = /2;x = -arccos(0,25)+2 n,
х=-(-arccos(0,25)) +2 n, n Z,
x = - arccos(0,25),
x = + arccos(0,25)
Ответ: а) /2+2 n,
-arccos(0,25)+2 n,
-(-arccos(0,25)) +2 n, n Z;
б) /2;
-arccos(0,25); +arccos(0,25)
Подготовка к профильному уровню единого государственного экзамена по математике. Полезные материалы по тригонометрии, большие теоретические видеолекции, видеоразборы задач и подборка заданий прошлых лет.
Полезные материалы
Подборки видео и онлайн-курсы
Тригонометрические формулы
Геометрическая иллюстрация тригонометрических формул
Арк-функции. Простейшие тригонометрические уравнения
Тригонометрические уравнения
- Необходимая теория для решения задач.
- а) Решите уравнение $7\cos^2 x - \cos x - 8 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -\dfrac{7\pi}{2}; -\dfrac{3\pi}{2} \right]$. - а) Решите уравнение $\dfrac{6}{\cos^2 x} - \dfrac{7}{\cos x} + 1 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -3\pi; -\pi \right]$. - Решите уравнение $\sin\sqrt{16 - x^2} = \dfrac12$.
- а) Решите уравнение $2\cos 2x - 12\cos x + 7 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -\pi; \dfrac{5\pi}{2} \right]$. - а) Решите уравнение $\dfrac{5}{\mathrm{tg}^2 x} - \dfrac{19}{\sin x} + 17 = 0$.
- Решите уравнение $\dfrac{2\cos^3 x + 3 \cos^2 x + \cos x}{\sqrt{\mathrm{ctg}x}} = 0$.
- Решите уравнение $\dfrac{\mathrm{tg}^3x - \mathrm{tg}x}{\sqrt{-\sin x}} = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -\dfrac{5\pi}{2}; -\pi \right)$.- а) Решите уравнение $\cos 2x = \sin\left(\dfrac{3\pi}{2} - x\right)$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ \dfrac{3\pi}{2}; \dfrac{5\pi}{2} \right]$. - а) Решите уравнение $2\sin^2\left(\dfrac{3\pi}{2} + x\right) = \sqrt3\cos x$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -\dfrac{7\pi}{2}; -2\pi \right]$.
Видеоразборы задач
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \sqrt{3}; \sqrt{20} \right]$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -\dfrac{9\pi}{2}; -3\pi \right]$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -\sqrt{3}; \sqrt{30} \right]$.
а) Решите уравнение $\cos 2x = 1 - \cos\left(\dfrac{\pi}{2} - x\right)$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -\dfrac{5\pi}{2}; -\pi \right)$.
а) Решите уравнение $\cos^2 (\pi - x) - \sin \left(x + \dfrac{3\pi}{2} \right) = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\dfrac{5\pi}{2}; 4\pi \right]$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\log_5 2; \log_5 20 \right]$.
а) Решите уравнение $8 \sin^2 x + 2\sqrt{3} \cos \left(\dfrac{3\pi}{2} - x\right) = 9$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[- \dfrac{5\pi}{2}; -\pi \right]$.
а) Решите уравнение $2\log_3^2 (2 \cos x) - 5\log_3 (2 \cos x) + 2 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\pi; \dfrac{5\pi}{2} \right]$.
а) Решите уравнение $\left(\dfrac{1}{49} \right)^{\sin x} = 7^{2 \sin 2x}$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\dfrac{3\pi}{2}; 3\pi \right]$.
а) Решите уравнение $\sin x + \left(\cos \dfrac{x}{2} - \sin \dfrac{x}{2}\right)\left(\cos \dfrac{x}{2} + \sin \dfrac{x}{2}\right) = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\pi; \dfrac{5\pi}{2}\right]$.
а) Решите уравнение $\log_4 (\sin x + \sin 2x + 16) = 2$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$.
Подборка заданий прошлых лет
- а) Решите уравнение $\dfrac{\sin x}{\sin^2\dfrac{x}{2}} = 4\cos^2\dfrac{x}{2}$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -\dfrac{9\pi}{2}; -3\pi \right]$. (ЕГЭ-2018. Досрочная волна) - а) Решите уравнение $\sqrt{x^3 - 4x^2 - 10x + 29} = 3 - x$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -\sqrt{3}; \sqrt{30} \right]$. (ЕГЭ-2018. Досрочная волна, резервный день) - а) Решите уравнение $2 \sin^2 x + \sqrt2 \sin \left(x + \dfrac{\pi}{4}\right) = \cos x $.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -2\pi; -\dfrac{\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $\sqrt6 \sin^2 x + \cos x = 2\sin\left(x + \dfrac{\pi}{6} \right)$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 3\pi; \dfrac{9\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $\sin x + 2\sin\left(2x + \dfrac{\pi}{6} \right) = \sqrt3 \sin 2x + 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -\dfrac{7\pi}{2}; -2\pi \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $\cos^2 x + \sin x = \sqrt2 \sin\left(x + \dfrac{\pi}{4} \right)$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2 \sin\left(2x + \dfrac{\pi}{3} \right) - \sqrt{3} \sin x = \sin 2x + \sqrt3$.
- а) Решите уравнение $2\sqrt3 \sin\left(x + \dfrac{\pi}{3} \right) - \cos 2x = 3\cos x - 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ 2\pi; \dfrac{7\pi}{2} \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2\sin\left(2x + \dfrac{\pi}{6} \right) - \cos x = \sqrt3\sin 2x - 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{5\pi}{2}; 4\pi \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $\sqrt2\sin\left(\dfrac{\pi}{4} + x \right) + \cos 2x = \sin x - 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{7\pi}{2}; 5\pi \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $\sqrt2\sin\left(2x + \dfrac{\pi}{4} \right) + \sqrt2\cos x = \sin 2x - 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -\dfrac{5\pi}{2}; -\pi \right]$. (ЕГЭ-2018. Основная волна) - а) Решите уравнение $2\sin\left(x + \dfrac{\pi}{3} \right) + \cos 2x = \sqrt3\cos x + 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -3\pi; -\dfrac{3\pi}{2} \right]$. (ЕГЭ-2018. Основная волна)
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \pi; \dfrac{5\pi}{2} \right]$. (ЕГЭ-2018. Основная волна)- а) Решите уравнение $2\sin\left(x + \dfrac{\pi}{4} \right) + \cos 2x = \sqrt2\cos x + 1$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \pi; \dfrac{5\pi}{2} \right]$. (ЕГЭ-2018. Основная волна, резервный день) - а) Решите уравнение $2\cos x - \sqrt3 \sin^2 x = 2\cos^3 x$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -\dfrac{7\pi}{2}; -2\pi \right]$. (ЕГЭ-2018. Основная волна, резервный день) - а) Решите уравнение $2\cos x + \sin^2 x = 2\cos^3 x$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -\dfrac{9\pi}{2}; -3\pi \right]$. (ЕГЭ-2018. Основная волна, резервный день) - а) Решите уравнение $2\sqrt2\sin \left(x + \dfrac{\pi}{3}\right) + 2\cos^2 x = 2 + \sqrt6 \cos x$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ -3\pi; -\dfrac{3\pi}{2} \right]$. (ЕГЭ-2018. Основная волна, резервный день) - а) Решите уравнение $x - 3\sqrt{x - 1} + 1 = 0$.
б) Найдите все корни этого уравнения, принадлежащие отрезку $\left[ \sqrt{3}; \sqrt{20} \right]$. (ЕГЭ-2018. Основная волна, резервный день) - а) Решите уравнение $2x \cos x - 8\cos x + x - 4 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -\dfrac{\pi}{2};\ \pi \right]$. (ЕГЭ-2017, основная волна, резервный день) - а) Решите уравнение $\log_3 (x^2 - 2x) = 1$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \log_2 0{,}2;\ \log_2 5 \right]$. (ЕГЭ-2017, основная волна, резервный день) - а) Решите уравнение $\log_3 (x^2 - 24x) = 4$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \log_2 0{,}1;\ 12\sqrt{5} \right]$. (ЕГЭ-2017, основная волна, резервный день) - а) Решите уравнение $0{,}4^{\sin x} + 2{,}5^{\sin x} = 2$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ 2\pi;\ \dfrac{7\pi}{2} \right]$. (ЕГЭ-2017, основная волна) - а) Решите уравнение $\log_8 \left(7\sqrt{3} \sin x - \cos 2x - 10\right) = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{3\pi}{2};\ 3\pi \right]$. (ЕГЭ-2017, основная волна) - а) Решите уравнение $\log_4 \left(2^{2x} - \sqrt{3} \cos x - 6\sin^2 x\right) = x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{5\pi}{2};\ 4\pi \right]$. (ЕГЭ-2017, основная волна) - а) Решите уравнение $2\log_2^2 \left(\sin x\right) - 5 \log_2 \left(\sin x\right) - 3 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ - 3\pi;\ - \dfrac{3\pi}{2} \right]$. (ЕГЭ-2017, основная волна) - а) Решите уравнение $81^{\cos x} - 12\cdot 9^{\cos x} + 27 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ - 4\pi;\ - \dfrac{5\pi}{2} \right]$. (ЕГЭ-2017, основная волна) - а) Решите уравнение $8^x - 9 \cdot 2^{x + 1} + 2^{5 - x} = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \log_5 2;\ \log_5 20 \right]$. (ЕГЭ-2017, досрочная волна) - а) Решите уравнение $2\log^2_9 x - 3 \log_9 x + 1 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \sqrt{10};\ \sqrt{99} \right]$. (ЕГЭ-2016, основная волна, резервный день) - а) Решите уравнение $6\log^2_8 x - 5 \log_8 x + 1 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ 2;\ 2{,}5 \right]$. (ЕГЭ-2016, основная волна, резервный день) - а) Решите уравнение $\sin 2x = 2\sin x + \sin \left(x + \dfrac{3\pi}{2} \right) + 1$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -4\pi;\ -\dfrac{5\pi}{2} \right]$. (ЕГЭ-2016, основная волна, резервный день) - а) Решите уравнение $2\cos^2 x + 1 = 2\sqrt{2} \cos \left(\dfrac{3\pi}{2} - x \right)$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{3\pi}{2};\ 3\pi \right]$. (ЕГЭ-2016, основная волна) - а) Решите уравнение $2\log^2_2 (2\cos x) - 9 \log_2 (2\cos x) + 4 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -2\pi;\ -\dfrac{\pi}{2} \right]$. (ЕГЭ-2016, основная волна) - а) Решите уравнение $8^x - 7 \cdot 4^x - 2^{x + 4} + 112 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \log_2 5;\ \log_2 11 \right]$. (ЕГЭ-2016, досрочная волна) - а) Решите уравнение $\cos 2x + \cos^2 \left(\dfrac{3\pi}{2} - x \right) = 0,25$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -4\pi;\ -\dfrac{5\pi}{2} \right]$. (ЕГЭ-2016, досрочная волна) - а) Решите уравнение $\dfrac{13\sin^2 x - 5\sin x}{13\cos x + 12} = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -3\pi;\ -\dfrac{3\pi}{2} \right]$. (ЕГЭ-2016, досрочная волна) - а) Решите уравнение $\dfrac{\sin2x}{\sin\left(\dfrac{7\pi}{2} - x \right)} = \sqrt{2}$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left$. (ЕГЭ-2015, основная волна) - а) Решите уравнение $4 \sin^2 x = \mathrm{tg} x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ - \pi;\ 0\right]$. (ЕГЭ-2015, основная волна) - а) Решите уравнение $3\cos 2x - 5\sin x + 1 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \pi;\ \dfrac{5\pi}{2}\right]$. (ЕГЭ-2015, основная волна) - а) Решите уравнение $\cos 2x - 5\sqrt{2}\cos x - 5 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -3\pi;\ -\dfrac{3\pi}{2}\right]$. (ЕГЭ-2015, основная волна) - а) Решите уравнение $\sin 2x + \sqrt{2} \sin x = 2\cos x + \sqrt{2}$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \pi;\ \dfrac{5\pi}{2}\right]$. (ЕГЭ-2015, досрочная волна) - а) Решите уравнение $2\cos^3 x - \cos^2 x + 2\cos x - 1 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ 2\pi;\ \dfrac{7\pi}{2}\right]$. (ЕГЭ-2015, досрочная волна) - а) Решите уравнение $\mathrm{tg}^2 x + (1 + \sqrt{3}) \mathrm{tg} x + \sqrt{3} = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{5\pi}{2}; \ 4\pi\right]$. (ЕГЭ-2014, основная волна) - а) Решите уравнение $2\sqrt{3} \cos^2\left(\dfrac{3\pi}{2} + x\right) - \sin 2x = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{3\pi}{2}; \ 3\pi\right]$. (ЕГЭ-2014, основная волна) - а) Решите уравнение $\cos 2x + \sqrt{2} \sin\left(\dfrac{\pi}{2} + x\right) + 1 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -3\pi; \ -\dfrac{3\pi}{2}\right]$. (ЕГЭ-2014, основная волна) - а) Решите уравнение $-\sqrt{2} \sin\left(-\dfrac{5\pi}{2} + x\right) \cdot \sin x = \cos x$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{9\pi}{2}; \ 6\pi\right]$. (ЕГЭ-2014, досрочная волна) - а) Решите уравнение $\sin 2x = \sin\left(\dfrac{\pi}{2} + x\right)$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -\dfrac{7\pi}{2}; \ -\dfrac{5\pi}{2}\right]$. (ЕГЭ-2013, основная волна) - а) Решите уравнение $6 \sin^2 x + 5\sin\left(\dfrac{\pi}{2} - x\right) - 2 = 0$.
б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -5\pi; \ - \dfrac{7\pi}{2}\right]$. (ЕГЭ-2012, вторая волна)
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение : с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
А) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]
Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
Sqrt(2)cos^2x = cosx
Sqrt(2)cos^2x - cosx = 0
Cosx(sqrt(2)cosx - 1) = 0
X1 = Pi/2 + Pin, n ∈ Z
Sqrt(2)cosx - 1 = 0
Cosx = 1/sqrt(2)
Cosx = sqrt(2)/2
X2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z
X2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z
Решим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
7/2 меньше или равно 1/2 + n меньше или равно -2
7/2 - 1/2 меньше или равно n меньше или равно -2 - 1/2
4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8
Целых n в этом промежутке нет
7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8
Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
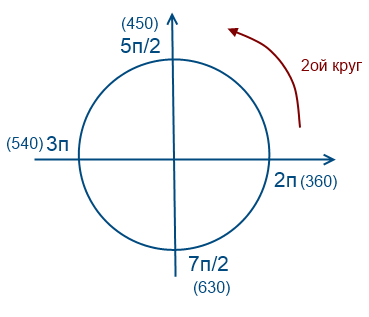
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)

Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 - 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 - 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 - 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.

Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
