Признаки возрастания и убывания функций. Признаки локального возрастания и убывания функции
Чтобы определить характер функции и говорить о ее поведении, необходимо находить промежутки возрастания и убывания. Этот процесс получил название исследования функции и построения графика. Точка экстремума используется при нахождении наибольшего и наименьшего значения функции, так как в них происходит возрастание или убывание функции из интервала.
Данная статья раскрывает определения, формулируем достаточный признак возрастания и убывания на интервале и условие существования экстремума. Это применимо к решению примеров и задач. Следует повторить раздел дифференцирования функций, потому как при решении необходимо будет использовать нахождение производной.
Yandex.RTB R-A-339285-1 Определение 1
Функция y = f (x) будет возрастать на интервале x , когда при любых x 1 ∈ X и x 2 ∈ X , x 2 > x 1 неравенство f (x 2) > f (x 1) будет выполнимо. Иначе говоря, большему значению аргумента соответствует большее значение функции.
Определение 2
Функция y = f (x) считается убывающей на интервале x , когда при любых x 1 ∈ X , x 2 ∈ X , x 2 > x 1 равенство f (x 2) > f (x 1) считается выполнимым. Иначе говоря, большему значению функции соответствует меньшее значение аргумента. Рассмотрим рисунок, приведенный ниже.
Замечание: Когда функция определенная и непрерывная в концах интервала возрастания и убывания, то есть (a ; b) , где х = а, х = b , точки включены в промежуток возрастания и убывания. Определению это не противоречит, значит, имеет место быть на промежутке x .
Основные свойства элементарных функций типа y = sin x – определенность и непрерывность при действительных значениях аргументах. Отсюда получаем, что возрастание синуса происходит на интервале - π 2 ; π 2 , тогда возрастание на отрезке имеет вид - π 2 ; π 2 .
Определение 3Точка х 0 называется точкой максимума для функции y = f (x) , когда для всех значений x неравенство f (x 0) ≥ f (x) является справедливым. Максимум функции – это значение функции в точке, причем обозначается y m a x .
Точка х 0 называется точкой минимума для функции y = f (x) , когда для всех значений x неравенство f (x 0) ≤ f (x) является справедливым. Минимум функции – это значение функции в точке, причем имеет обозначение вида y m i n .
Окрестностями точки х 0 считаются точки экстремума, а значение функции, которое соответствует точкам экстремума. Рассмотрим рисунок, приведенный ниже.

Экстремумы функции с набольшим и с наименьшим значением функции. Рассмотрим рисунок, приведенный ниже.

Первый рисунок говорит о том, что необходимо найти наибольшее значение функции из отрезка [ a ; b ] . Оно находится при помощи точек максимума и равняется максимальному значению функции, а второй рисунок больше походит на поиск точки максимума при х = b .
Достаточные условия возрастания и убывания функции
Чтобы найти максимумы и минимумы функции, необходимо применять признаки экстремума в том случае, когда функция удовлетворяет этим условиям. Самым часто используемым считается первый признак.
Первое достаточное условие экстремума
Определение 4Пусть задана функция y = f (x) , которая дифференцируема в ε окрестности точки x 0 , причем имеет непрерывность в заданной точке x 0 . Отсюда получаем, что
- когда f " (x) > 0 с x ∈ (x 0 - ε ; x 0) и f " (x) < 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой максимума;
- когда f " (x) < 0 с x ∈ (x 0 - ε ; x 0) и f " (x) > 0 при x ∈ (x 0 ; x 0 + ε) , тогда x 0 является точкой минимума.
Иначе говоря, получим их условия постановки знака:
- когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком, то есть с + на - , значит, точка называется максимумом;
- когда функция непрерывна в точке x 0 , тогда имеет производную с меняющимся знаком с - на + , значит, точка называется минимумом.
Чтобы верно определить точки максимума и минимума функции, необходимо следовать алгоритму их нахождения:
- найти область определения;
- найти производную функции на этой области;
- определить нули и точки, где функция не существует;
- определение знака производной на интервалах;
- выбрать точки, где функция меняет знак.
Рассмотрим алгоритм на примере решения нескольких примеров на нахождение экстремумов функции.
Пример 1
Найти точки максимума и минимума заданной функции y = 2 (x + 1) 2 x - 2 .
Решение
Область определения данной функции – это все действительные числа кроме х = 2 . Для начала найдем производную функции и получим:
y " = 2 x + 1 2 x - 2 " = 2 · x + 1 2 " · (x - 2) - (x + 1) 2 · (x - 2) " (x - 2) 2 = = 2 · 2 · (x + 1) · (x + 1) " · (x - 2) - (x + 1) 2 · 1 (x - 2) 2 = 2 · 2 · (x + 1) · (x - 2) - (x + 2) 2 (x - 2) 2 = = 2 · (x + 1) · (x - 5) (x - 2) 2
Отсюда видим, что нули функции – это х = - 1 , х = 5 , х = 2 , то есть каждую скобку необходимо приравнять к нулю. Отметим на числовой оси и получим:

Теперь определим знаки производной из каждого интервала. Необходимо выбрать точку, входящую в интервал, подставить в выражение. Например, точки х = - 2 , х = 0 , х = 3 , х = 6 .
Получаем, что
y " (- 2) = 2 · (x + 1) · (x - 5) (x - 2) 2 x = - 2 = 2 · (- 2 + 1) · (- 2 - 5) (- 2 - 2) 2 = 2 · 7 16 = 7 8 > 0 , значит, интервал - ∞ ; - 1 имеет положительную производную. Аналогичным образом получаем, что
y " (0) = 2 · (0 + 1) · 0 - 5 0 - 2 2 = 2 · - 5 4 = - 5 2 < 0 y " (3) = 2 · (3 + 1) · (3 - 5) (3 - 2) 2 = 2 · - 8 1 = - 16 < 0 y " (6) = 2 · (6 + 1) · (6 - 5) (6 - 2) 2 = 2 · 7 16 = 7 8 > 0
Так как второй интервал получился меньше нуля, значит, производная на отрезке будет отрицательной. Третий с минусом, четвертый с плюсом. Для определения непрерывности необходимо обратить внимание на знак производной, если он меняется, тогда это точка экстремума.
Получим, что в точке х = - 1 функция будет непрерывна, значит, производная изменит знак с + на - . По первому признаку имеем, что х = - 1 является точкой максимума, значит получаем
y m a x = y (- 1) = 2 · (x + 1) 2 x - 2 x = - 1 = 2 · (- 1 + 1) 2 - 1 - 2 = 0
Точка х = 5 указывает на то, что функция является непрерывной, а производная поменяет знак с – на +. Значит, х=-1 является точкой минимума, причем ее нахождение имеет вид
y m i n = y (5) = 2 · (x + 1) 2 x - 2 x = 5 = 2 · (5 + 1) 2 5 - 2 = 24
Графическое изображение

Ответ: y m a x = y (- 1) = 0 , y m i n = y (5) = 24 .
Стоит обратить внимание на то, что использование первого достаточного признака экстремума не требует дифференцируемости функции с точке x 0 , этим и упрощает вычисление.
Пример 2
Найти точки максимума и минимума функции y = 1 6 x 3 = 2 x 2 + 22 3 x - 8 .
Решение.
Область определения функции – это все действительные числа. Это можно записать в виде системы уравнений вида:
1 6 x 3 - 2 x 2 - 22 3 x - 8 , x < 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 , x ≥ 0
После чего необходимо найти производную:
y " = 1 6 x 3 - 2 x 2 - 22 3 x - 8 " , x < 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 " , x > 0 y " = - 1 2 x 2 - 4 x - 22 3 , x < 0 1 2 x 2 - 4 x + 22 3 , x > 0
Точка х = 0 не имеет производной, потому как значения односторонних пределов разные. Получим, что:
lim y " x → 0 - 0 = lim y x → 0 - 0 - 1 2 x 2 - 4 x - 22 3 = - 1 2 · (0 - 0) 2 - 4 · (0 - 0) - 22 3 = - 22 3 lim y " x → 0 + 0 = lim y x → 0 - 0 1 2 x 2 - 4 x + 22 3 = 1 2 · (0 + 0) 2 - 4 · (0 + 0) + 22 3 = + 22 3
Отсюда следует, что функция непрерывна в точке х = 0 , тогда вычисляем
lim y x → 0 - 0 = lim x → 0 - 0 - 1 6 x 3 - 2 x 2 - 22 3 x - 8 = = - 1 6 · (0 - 0) 3 - 2 · (0 - 0) 2 - 22 3 · (0 - 0) - 8 = - 8 lim y x → 0 + 0 = lim x → 0 - 0 1 6 x 3 - 2 x 2 + 22 3 x - 8 = = 1 6 · (0 + 0) 3 - 2 · (0 + 0) 2 + 22 3 · (0 + 0) - 8 = - 8 y (0) = 1 6 x 3 - 2 x 2 + 22 3 x - 8 x = 0 = 1 6 · 0 3 - 2 · 0 2 + 22 3 · 0 - 8 = - 8
Необходимо произвести вычисления для нахождения значения аргумента, когда производная становится равной нулю:
1 2 x 2 - 4 x - 22 3 , x < 0 D = (- 4) 2 - 4 · - 1 2 · - 22 3 = 4 3 x 1 = 4 + 4 3 2 · - 1 2 = - 4 - 2 3 3 < 0 x 2 = 4 - 4 3 2 · - 1 2 = - 4 + 2 3 3 < 0
1 2 x 2 - 4 x + 22 3 , x > 0 D = (- 4) 2 - 4 · 1 2 · 22 3 = 4 3 x 3 = 4 + 4 3 2 · 1 2 = 4 + 2 3 3 > 0 x 4 = 4 - 4 3 2 · 1 2 = 4 - 2 3 3 > 0
Все полученные точки нужно отметить на прямой для определения знака каждого интервала. Поэтому необходимо вычислить производную в произвольных точках у каждого интервала. Например, у нас можно взять точки со значениями x = - 6 , x = - 4 , x = - 1 , x = 1 , x = 4 , x = 6 . Получим, что
y " (- 6) = - 1 2 x 2 - 4 x - 22 3 x = - 6 = - 1 2 · - 6 2 - 4 · (- 6) - 22 3 = - 4 3 < 0 y " (- 4) = - 1 2 x 2 - 4 x - 22 3 x = - 4 = - 1 2 · (- 4) 2 - 4 · (- 4) - 22 3 = 2 3 > 0 y " (- 1) = - 1 2 x 2 - 4 x - 22 3 x = - 1 = - 1 2 · (- 1) 2 - 4 · (- 1) - 22 3 = 23 6 < 0 y " (1) = 1 2 x 2 - 4 x + 22 3 x = 1 = 1 2 · 1 2 - 4 · 1 + 22 3 = 23 6 > 0 y " (4) = 1 2 x 2 - 4 x + 22 3 x = 4 = 1 2 · 4 2 - 4 · 4 + 22 3 = - 2 3 < 0 y " (6) = 1 2 x 2 - 4 x + 22 3 x = 6 = 1 2 · 6 2 - 4 · 6 + 22 3 = 4 3 > 0
Изображение на прямой имеет вид
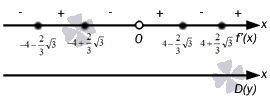
Значит, приходим к тому, что необходимо прибегнуть к первому признаку экстремума. Вычислим и получим, что
x = - 4 - 2 3 3 , x = 0 , x = 4 + 2 3 3 , тогда отсюда точки максимума имеют значени x = - 4 + 2 3 3 , x = 4 - 2 3 3
Перейдем к вычислению минимумов:
y m i n = y - 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 0 = - 8 y m i n = y 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 + 2 3 3 = - 8 27 3
Произведем вычисления максимумов функции. Получим, что
y m a x = y - 4 + 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 1 6 x 3 - 2 2 + 22 3 x - 8 x = 4 - 2 3 3 = 8 27 3
Графическое изображение

Ответ:
y m i n = y - 4 - 2 3 3 = - 8 27 3 y m i n = y (0) = - 8 y m i n = y 4 + 2 3 3 = - 8 27 3 y m a x = y - 4 + 2 3 3 = 8 27 3 y m a x = y 4 - 2 3 3 = 8 27 3
Если задана функция f " (x 0) = 0 , тогда при ее f "" (x 0) > 0 получаем, что x 0 является точкой минимума, если f "" (x 0) < 0 , то точкой максимума. Признак связан с нахождением производной в точке x 0 .
Пример 3
Найти максимумы и минимумы функции y = 8 x x + 1 .
Решение
Для начала находим область определения. Получаем, что
D (y) : x ≥ 0 x ≠ - 1 ⇔ x ≥ 0
Необходимо продифференцировать функцию, после чего получим
y " = 8 x x + 1 " = 8 · x " · (x + 1) - x · (x + 1) " (x + 1) 2 = = 8 · 1 2 x · (x + 1) - x · 1 (x + 1) 2 = 4 · x + 1 - 2 x (x + 1) 2 · x = 4 · - x + 1 (x + 1) 2 · x
При х = 1 производная становится равной нулю, значит, точка является возможным экстремумом. Для уточнения необходимо найти вторую производную и вычислить значение при х = 1 . Получаем:
y "" = 4 · - x + 1 (x + 1) 2 · x " = = 4 · (- x + 1) " · (x + 1) 2 · x - (- x + 1) · x + 1 2 · x " (x + 1) 4 · x = = 4 · (- 1) · (x + 1) 2 · x - (- x + 1) · x + 1 2 " · x + (x + 1) 2 · x " (x + 1) 4 · x = = 4 · - (x + 1) 2 x - (- x + 1) · 2 x + 1 (x + 1) " x + (x + 1) 2 2 x (x + 1) 4 · x = = - (x + 1) 2 x - (- x + 1) · x + 1 · 2 x + x + 1 2 x (x + 1) 4 · x = = 2 · 3 x 2 - 6 x - 1 x + 1 3 · x 3 ⇒ y "" (1) = 2 · 3 · 1 2 - 6 · 1 - 1 (1 + 1) 3 · (1) 3 = 2 · - 4 8 = - 1 < 0
Значит, использовав 2 достаточное условие экстремума, получаем, что х = 1 является точкой максимума. Иначе запись имеет вид y m a x = y (1) = 8 1 1 + 1 = 4 .
Графическое изображение

Ответ: y m a x = y (1) = 4 ..
Определение 5Функция y = f (x) имеет ее производную до n -го порядка в ε окрестности заданной точки x 0 и производную до n + 1 -го порядка в точке x 0 . Тогда f " (x 0) = f "" (x 0) = f " " " (x 0) = . . . = f n (x 0) = 0 .
Отсюда следует, что когда n является четным числом, то x 0 считается точкой перегиба, когда n является нечетным числом, то x 0 точка экстремума, причем f (n + 1) (x 0) > 0 , тогда x 0 является точкой минимума, f (n + 1) (x 0) < 0 , тогда x 0 является точкой максимума.
Пример 4
Найти точки максимума и минимума функции y y = 1 16 (x + 1) 3 (x - 3) 4 .
Решение
Исходная функция – целая рациональная, отсюда следует, что область определения – все действительные числа. Необходимо продифференцировать функцию. Получим, что
y " = 1 16 x + 1 3 " (x - 3) 4 + (x + 1) 3 x - 3 4 " = = 1 16 (3 (x + 1) 2 (x - 3) 4 + (x + 1) 3 4 (x - 3) 3) = = 1 16 (x + 1) 2 (x - 3) 3 (3 x - 9 + 4 x + 4) = 1 16 (x + 1) 2 (x - 3) 3 (7 x - 5)
Данная производная обратится в ноль при x 1 = - 1 , x 2 = 5 7 , x 3 = 3 . То есть точки могут быть точками возможного экстремума. Необходимо применить третье достаточное условие экстремума. Нахождение второй производной позволяет в точности определить наличие максимума и минимума функции. Вычисление второй производной производится в точках ее возможного экстремума. Получаем, что
y "" = 1 16 x + 1 2 (x - 3) 3 (7 x - 5) " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) y "" (- 1) = 0 y "" 5 7 = - 36864 2401 < 0 y "" (3) = 0
Значит, что x 2 = 5 7 является точкой максимума. Применив 3 достаточный признак, получаем, что при n = 1 и f (n + 1) 5 7 < 0 .
Необходимо определить характер точек x 1 = - 1 , x 3 = 3 . Для этого необходимо найти третью производную, вычислить значения в этих точках. Получаем, что
y " " " = 1 8 (x + 1) (x - 3) 2 (21 x 2 - 30 x - 3) " = = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) y " " " (- 1) = 96 ≠ 0 y " " " (3) = 0
Значит, x 1 = - 1 является точкой перегиба функции, так как при n = 2 и f (n + 1) (- 1) ≠ 0 . Необходимо исследовать точку x 3 = 3 . Для этого находим 4 производную и производим вычисления в этой точке:
y (4) = 1 8 (x - 3) (105 x 3 - 225 x 2 - 45 x + 93) " = = 1 2 (105 x 3 - 405 x 2 + 315 x + 57) y (4) (3) = 96 > 0
Из выше решенного делаем вывод, что x 3 = 3 является точкой минимума функции.
Графическое изображение

Ответ: x 2 = 5 7 является точкой максимума, x 3 = 3 - точкой минимума заданной функции.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Определение возрастающей функции.
Функция y=f(x)
возрастает
на интервале X
,
если для любых и ![]() выполняется
неравенство .
Другими словами – большему значению
аргумента соответствует большее значение
функции.
выполняется
неравенство .
Другими словами – большему значению
аргумента соответствует большее значение
функции.
Определение убывающей функции.
Функция y=f(x)
убывает
на интервале X
,
если для любых и ![]() выполняется
неравенство
выполняется
неравенство ![]() .
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
.
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.

ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a;b) , то есть при x=a и x=b , то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X .
К примеру, из свойств основных элементарных функций мы знаем, что y=sinx определена и непрерывна для всех действительных значений аргумента. Поэтому, из возрастания функции синуса на интервале мы можем утверждать о возрастании на отрезке .
Точки экстремума, экстремумы функции.
Точку называют точкой максимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называютмаксимумом функции и обозначают .
Точку называют точкой минимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называютминимумом функции и обозначают .
Под
окрестностью точки понимают
интервал ![]() ,
где -
достаточно малое положительное число.
,
где -
достаточно малое положительное число.
Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .

Не путайте экстремумы функции с наибольшим и наименьшим значением функции.

На первом рисунке наибольшее значение функции на отрезке достигается в точке максимума и равно максимуму функции, а на втором рисунке – наибольшее значение функции достигается в точке x=b , которая не является точкой максимума.
Достаточные условия возрастания и убывания функции.
На основании достаточных условий (признаков) возрастания и убывания функции находятся промежутки возрастания и убывания функции.
Вот формулировки признаков возрастания и убывания функции на интервале:
если производная функции y=f(x) положительна для любого x из интервала X , то функция возрастает на X ;
если производная функции y=f(x) отрицательна для любого x из интервала X , то функция убывает на X .
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
Рассмотрим пример нахождения промежутков возрастания и убывания функции для разъяснения алгоритма.
Пример.
Найти промежутки возрастания и убывания функции .
Решение.
Первым шагом является нахождение обрасти определения функции. В нашем примере выражение в знаменателе не должно обращаться в ноль, следовательно, .
Переходим
к нахождению производной функции:

Для
определения промежутков возрастания
и убывания функции по достаточному
признаку решаем неравенства и на
области определения. Воспользуемся
обобщением метода интервалов. Единственным
действительным корнем числителя
является x
= 2
,
а знаменатель обращается в ноль при x=0
.
Эти точки разбивают область определения
на интервалы, в которых производная
функции сохраняет знак. Отметим эти
точки на числовой прямой. Плюсами и
минусами условно обозначим интервалы,
на которых производная положительна
или отрицательна. Стрелочки снизу
схематично показывают возрастание или
убывание функции на соответствующем
интервале.

Очень важную информацию о поведении функции предоставляют промежутки возрастания и убывания. Их нахождение является частью процесса исследования функции и построения графика . К тому же точкам экстремума, в которых происходит смена с возрастания на убывание или с убывания на возрастание, уделяется особое внимание при нахождении наибольшего и наименьшего значения функции на некотором интервале.
В этой статье дадим необходимые определения, сформулируем достаточный признак возрастания и убывания функции на интервале и достаточные условия существования экстремума, применим всю эту теорию к решению примеров и задач.
Навигация по странице.
Возрастание и убывание функции на интервале.
Определение возрастающей функции.
Функция y=f(x)
возрастает на интервале X
, если для любых и ![]() выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Определение убывающей функции.
Функция y=f(x)
убывает на интервале X
, если для любых и ![]() выполняется неравенство
выполняется неравенство ![]() . Другими словами – большему значению аргумента соответствует меньшее значение функции.
. Другими словами – большему значению аргумента соответствует меньшее значение функции.

ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a;b) , то есть при x=a и x=b , то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X .
К примеру, из свойств основных элементарных функций мы знаем, что y=sinx определена и непрерывна для всех действительных значений аргумента. Поэтому, из возрастания функции синуса на интервале мы можем утверждать о возрастании на отрезке .
Точки экстремума, экстремумы функции.
Точку называют точкой максимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают .
Точку называют точкой минимума функции y=f(x) , если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .
Под окрестностью точки понимают интервал ![]() , где - достаточно малое положительное число.
, где - достаточно малое положительное число.
Точки минимума и максимума называют точками экстремума , а значения функции, соответствующие точкам экстремума, называют экстремумами функции .

Не путайте экстремумы функции с наибольшим и наименьшим значением функции.

На первом рисунке наибольшее значение функции на отрезке достигается в точке максимума и равно максимуму функции, а на втором рисунке – наибольшее значение функции достигается в точке x=b , которая не является точкой максимума.
Достаточные условия возрастания и убывания функции.
На основании достаточных условий (признаков) возрастания и убывания функции находятся промежутки возрастания и убывания функции.
Вот формулировки признаков возрастания и убывания функции на интервале:
- если производная функции y=f(x) положительна для любого x из интервала X , то функция возрастает на X ;
- если производная функции y=f(x) отрицательна для любого x из интервала X , то функция убывает на X .
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
Рассмотрим пример нахождения промежутков возрастания и убывания функции для разъяснения алгоритма.
Пример.
Найти промежутки возрастания и убывания функции .
Решение.
На первом шаге нужно найти область определения функции . В нашем примере выражение в знаменателе не должно обращаться в ноль, следовательно, .
Переходим к нахождению производной функции:
Для определения промежутков возрастания и убывания функции по достаточному признаку решаем неравенства и на области определения. Воспользуемся обобщением метода интервалов. Единственным действительным корнем числителя является x = 2
, а знаменатель обращается в ноль при x=0
. Эти точки разбивают область определения на интервалы, в которых производная функции сохраняет знак. Отметим эти точки на числовой прямой. Плюсами и минусами условно обозначим интервалы, на которых производная положительна или отрицательна. Стрелочки снизу схематично показывают возрастание или убывание функции на соответствующем интервале.
Таким образом,  и
и  .
.
В точке x=2 функция определена и непрерывна, поэтому ее следует добавить и к промежутку возрастания и к промежутку убывания. В точке x=0 функция не определена, поэтому эту точку не включаем в искомые интервалы.
Приводим график функции для сопоставления с ним полученных результатов.

Ответ:
Функция возрастает при ![]() , убывает на интервале (0;2]
.
, убывает на интервале (0;2]
.
Достаточные условия экстремума функции.
Для нахождения максимумов и минимумов функции можно пользоваться любым из трех признаков экстремума, конечно, если функция удовлетворяет их условиям. Самым распространенным и удобным является первый из них.
Первое достаточное условие экстремума.
Пусть функция y=f(x) дифференцируема в -окрестности точки , а в самой точке непрерывна.
Другими словами:
Алгоритм нахождения точек экстремума по первому признаку экстремума функции.
- Находим область определения функции.
- Находим производную функции на области определения.
- Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (все перечисленные точки называют точками возможного экстремума , проходя через эти точки, производная как раз может изменять свой знак).
- Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала).
- Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак - они и являются точками экстремума.
Слишком много слов, рассмотрим лучше несколько примеров нахождения точек экстремума и экстремумов функции с помощью первого достаточного условия экстремума функции.
Пример.
Найти экстремумы функции .
Решение.
Областью определения функции является все множество действительных чисел, кроме x=2 .
Находим производную:
Нулями числителя являются точки x=-1
и x=5
, знаменатель обращается в ноль при x=2
. Отмечаем эти точки на числовой оси
Определяем знаки производной на каждом интервале, для этого вычислим значение производной в любой из точек каждого интервала, например, в точках x=-2, x=0, x=3 и x=6 .
Следовательно, на интервале производная положительна (на рисунке ставим знак плюс над этим интервалом). Аналогично
Поэтому над вторым интервалом ставим минус, над третьим – минус, над четвертым – плюс.
Осталось выбрать точки, в которых функция непрерывна и ее производная меняет знак. Это и есть точки экстремума.
В точке x=-1
функция непрерывна и производная меняет знак с плюса на минус, следовательно, по первому признаку экстремума, x=-1
– точка максимума, ей соответствуем максимум функции  .
.
В точке x=5
функция непрерывна и производная меняет знак с минуса на плюс, следовательно, x=-1
– точка минимума, ей соответствуем минимум функции  .
.
Графическая иллюстрация.

Ответ:
ОБРАТИТЕ ВНИМАНИЕ: первый достаточный признак экстремума не требует дифференцируемости функции в самой точке .
Пример.
Найдите точки экстремума и экстремумы функции ![]() .
.
Решение.
Областью определения функции является все множество действительных чисел. Саму функцию можно записать в виде:
Найдем производную функции:
В точке x=0
производная не существует, так как значения односторонних пределов при стремлении аргумента к нулю не совпадают:
В это же время, исходная функция является непрерывной в точке x=0
(смотрите раздел исследование функции на непрерывность):
Найдем значения аргумента, при котором производная обращается в ноль:
Отметим все полученные точки на числовой прямой и определим знак производной на каждом из интервалов. Для этого вычислим значения производной в произвольных точках каждого интервала, к примеру, при x=-6, x=-4, x=-1, x=1, x=4, x=6
.
То есть,
Таким образом, по первому признаку экстремума, точками минимума являются ![]() , точками максимума являются
, точками максимума являются ![]() .
.
Вычисляем соответствующие минимумы функции
Вычисляем соответствующие максимумы функции
Графическая иллюстрация.

Ответ:
 .
.
Второй признак экстремума функции.
Как видите, этот признак экстремума функции требует существования производной как минимум до второго порядка в точке .
Пусть f непрерывна на отрезке и дифференцируема во внутренних точках этого отрезка. Тогда существует внутренняя точка с этого отрезка, такая, что касательная к графику функции, проведенная в точке с абсциссой с, параллельна хорде АВ, где A(а;f(x)) и B(b;f(x)). Или: на гладкой дуге АВ всегда есть точка с, в которой касательная параллельна хорде, соединяющей концы дуги.
Пусть f непрерывна на отрезке и дифференцируема во внутренних точках этого отрезка. Тогда существует внутренняя точка с этого отрезка, такая, что
Следствие 1:если функция f непрерывна на отрезке , а её производная равна нулю внутри этого отрезка, то функция f постоянна на отрезке .
Следствие 2: Если функции f и g непрерывны на отрезке и имеют одинаковые производные внутри этого отрезка, то они отличаются постоянным слагаемым.
2. Достаточный признак возрастания функции:
Если f[/](x)>0 в каждой точке интервала I, то функция f возрастает на интервале I.
3. Достаточный признак убывания функции:
Если f[/](x)
Докажем эти признаки по формуле Лагранжа:
Возьмем два любых числа и из интервала. Пусть. По формуле Лагранжа существует число, такое, что.
Число c принадлежит интервалу I, так как точки и принадлежат этому интервалу. Если f[/](x)>0 для, то f[/](с) >0 , и поэтому - это следует из формулы (1), так как ->0. Этим доказано возрастание функций f на интервале I. Если же f[/](x) 0. Доказано убывание функции f на интервале I.
Пример 1. найдите промежутки возрастания и убывания функции
2. Найдем производную функции и ее критические точки: или
3. Отметим на числовой оси точки экстремумов и найдем промежутки возрастания и убывания функции
Ответ: - функция возрастает
Функция убывает
Пример 2. Исследуйте на возрастание (убывание) функцию:
2. Найдем производную и точки экстремумов функции:
3. Отметим критическую точку на числовой оси и найдем промежутки возрастания (убывания) функции:
Ответ: - функция убывает
Функция возрастает
II. Критические точки. Признаки нахождения максимума и минимума функции.
1. Критические точки
Определение: критические точки функции - это внутренние точки области определения функции, в которых её производная равна нулю или не существует.
№1. Найдите критические точки функции f: а) g(x) =
Ответ: , где; , где б) g(x) =
2. Признаки нахождения максимума и минимума функции.
Признак максимума функций:
Если функция f непрерывна в точке х0 , а f[/](x)>0 на интервале (а;х0) и f[/](x)
Или: если в точке х0 производная меняет знак с плюса на минус, то х0 есть точка максимума.
Доказательство:
Производная f[/](x)>0 на интервале (а;х0), а функция непрерывна в точке х0 ,следовательно функция f возрастает на промежутке (a; х0], и потому f(x)
На промежутке [х0;в) функция убывает, и потому f(x)
Признаки минимума функции:
Если функция f непрерывна в точке х0 , а f[/](x) 0 на интервале (х0;в), то точка х0 является точкой минимума функции f.
Или: если в точке х0 производная меняет знак с минуса на плюс, то х0 есть точка минимума.
Доказательство:
Производная f[/](x) f (x0) для всех х из интервала (а;х0).
На промежутке [х0;в) функция f возрастает, и потому f(x) >f (x0) для всех из интервала (а;в), то есть х0 есть точка минимума f.
III. Вторая производная. Признаки выпуклости и вогнутости.
Пусть и в точке существует вторая производная. Тогда, если, то точка является точкой минимума, а если, то точка является точкой максимума функции.
Если, то выпуклость направлена вниз. Если, то выпуклость направлена вверх.
IV. Наклонные асимптоты
Определение: Прямая является наклонной асимптотой графика функции, где и
Уравнение наклонной асимптоты
Вертикальные асимптоты уравнение наклонной асимптоты
V. План исследования функции
1. Найдем область определения функции.
2. Исследовать функцию на четность (нечетность).
3. Найти точки пересечения графика с осями координат и определить интервалы знакопостоянства функции.
4. Найти производную.
5. Найти точки экстремума функции и интервалы возрастания и убывания функции.
6. Составить таблицу.
7. Найти вторую производную.
8. Найти точки перегиба графика функции и установить интервалы выпуклости и вогнутости этого графика.
9. Найти асимптоты графика функции, если это необходимо.
10. Построить эскиз графика данной функции.
11. Найти множество значений функции.
VI. Примеры на исследование функции
2). О четности функции говорить нельзя.
5) Найдем точки экстремума функции и интервалы возрастания и убывания функции:
Функция возрастает
Функция убывает
6) Составим таблицу х
7) Найдем вторую производную
8) Найдем точки перегиба: или
Выпуклость вверх
Выпуклость вниз
9) Найдем наклонные асимптоты не существует. наклонных асимптот нет.
10) График
; х=2 - вертикальная асимптота
2). О четности функции говорить нельзя
3) Найдем точки пересечения графика с осью ОХ.
Найдем точки пересечения графика с осью ОУ.
4) Найдем производную функции:
5) Найдем точки экстремума функции и точки возрастания и убывания функции:
Функция возрастает
Функция убывает
6) Составим таблицу х
7) Найдем вторую производную:
8) Найдем точки перегиба: точек перегиба нет
Выпуклость вниз
Выпуклость вверх
Уравнение наклонной асимптоты
10) График
Вертикальная асимптота
2) о четности функции говорить нельзя
Точек пересечения с осью OX нет.
Не существует. Таких точек нет.
4) Найдем производную:
Функция убывает
Функция возрастает
6) Составим таблицу:
7) Построим график функции:
Вертикальная асимптота
2) - о четности функции говорить нельзя
3) Найдем точки пересечения графика с осью OX.
Найдем точки пересечения графика с осью OY.
4) Найдем производную:
5) Найдем точки экстремума функции и интервалы возрастания и убывания функции.
Критических точек нет.
Точек max и min нет.
6) Составим таблицу:
↘ 7) Найдем вторую производную:
8) Найдем точки перегиба графика функции и установим интервалы выпуклости и вогнутости:
Точек перегиба нет.
Выпуклость вверх
Выпуклость вниз
9) Найдем наклонные асимптоты:
Уравнение горизонтальной асимптоты, т. к. k = 0.
10) Построим график функции:
; - вертикальные асимптоты
2) - функция нечетная, так как. График симметричен относительно начала координат.
3) Найдем точки пересечения графика с осью OX.
Найдем точки пересечения графика с осью OY.
4) Найдем производную:
5) Найдем точки экстремума и интервалы возрастания и убывания функции:
Нет решения.
Функция убывает
Функция возрастает
6) Составим таблицу:
↘ Не сущ.
↗ 7) Найдем наклонные асимптоты:
Наклонных асимптот нет.
8) Найдем вторую производную:
9) Найдем точки перегиба: или или
Выпуклость вниз
Выпуклость вверх
10) Построим график
VII. Историческая справка.
Совсем иным был конец жизненного пути другого творца математического анализа - Готфрида Вильгельма Лей - бница (1646 - 1716). Но обо всем по порядку.
Его предки были выходцами из Польши и носили фамилию Любениц. После переселения в Лейпциг" фамилия их стала произноситься на немецкий лад. Интересно отметить, что и само название этого города тоже славянское, оно означает >. Лейбниц родился в семье профессора философии Лейпцигского университета. Он рано лишился родителей: в 6 лет остался без отца, а в 17 - без матери. В школьные годы Лейбниц поражал своих учителей умением слагать стихи на латинском и греческом языках, увлеченностью философией и математикой. Он отличался большой любознательностью, многие предметы изучал самостоятельно, до знакомства с ними в школе. Память у него была неровной: легко запоминал сложные вещи и хуже - простые; не мог долго производить вычисления, но тяготел к обобщениям и абстракциям. И такая память и склад мышления сохранились у Лейбница на всю жизнь.
В 15. лет Лейбниц - студент философского факультета Лейпцигского университета. Этот факультет был подготовитель - ным для юридического и богословского. Закончив с блеском философский, а затем юридический факультет, 20-летний Лейбниц не смог получить желаемой должности в родном городе. Консервативные порядки в университете ставили материальные преграды к получению докторской степени. Он едет в Нюрнберг и в тамошнем университете с небывалым успехом защищает юридическую диссертацию на степень доктора. Необычайный талант молодого ученого был замечен. Его приглашает на дипломатическую службу курфюрст (князь, имеющий право выбора короля) города Майнца, а позже - ганноверский герцог.
Находясь по делам курфюрста в Париже, Лейбниц встречается со многими известными учеными. Обсуждения различных проблем пробуждают в нем интерес к математике. Позже в письме к И. Бернулли он вспоминал: >. По окончании универси - тета (1666) Лейбниц опубликовал философско-математическую работу >, так что, говоря о своем >, он имел в виду неосведомленность о последних достижениях математики. Чтобы познакомиться с новыми результатами и идеями, возникшими в то время в математике, он обращается за помощью к Гюйгенсу. Тот советует ему внимательно изучить ряд работ, и Лейбниц с завидным рвением берется за дело: изучает труды Сен-Винцента и Валлиса, Декарта и Паскаля, занимается собственными исследованиями.
Но когда он по дипломатическим делам попадает в Лондон и сообщает о своих результатах английским математикам, то с удивлением узнает, что многие из этих результатов им уже известны из рукописи Ньютона >, хранящейся в Королевском обществе. Лейбниц через секретаря этого общества Ольденбурга (1615 - 1677) пишет Ньютону о своих работах. В том же письме он просит Ньютона сообщить его результаты. В ответ он получает (опять через Ольденбурга) два письма, в которых Ньютон разъясняет операции дифференцирования и интегрирования с помощью рядов.
Лейбниц не спешил обнародовать свои результаты в области нового исчисления, возможно, ожидая публикаций Ньютона. Но в 1683 г. Чирнгауз печатает статью о квадратуре алгебраических кривых. В ней не упоминается имя Лейбница, хотя в решении этих вопросов Чирнгауз многим был ему обязан. Чтобы сохранить пальму первенства в этой области, Лейбниц в следующем году печатает статью >, а через год - >. В первой из них содержались основы дифференциального исчисления, во второй - интегрального.
В основу новой науки он положил понятие дифференциала. Сейчас дифференциал df(x0) функции y=f(x) в точке х0 задается формулой df(xo) = f"(xo)dx, где f"(xb) - производная, вычисленная в точке хо, их - приращение аргумента. У Лейбница дифферен - циал определяется как один из катетов характеристического треугольника, о котором шла речь в предыдущей главе (п. 9). Из рисунка 46 видно, что эти определения эквивалентны.
Лейбниц дает правила вычисления дифференциала суммы, разности, произведения, частного, степени, решает дифференци - альные уравнения. Интеграл он определяет как сумму дифференци - алов, подчеркивая взаимную обратность операций дифференциро - вания и интегрирования: >. Откуда вытекают свойст - ва интегралов и способы их вычисле - ния. В последующих статьях Лейбниц развил новый анализ. Он доказал, что любая интегрируемая функция являет - ся ограниченной (необходимое усло - вие интегрируемости), разработал ал - горитм вычисления некоторых типов интегралов, в частности способ интег - рирования рациональных функций. Значение этого способа невозможно переоценить, так как с помощью раз - личных подстановок к интегралам от рациональных функций сводится масса самых разнообразных интегралов. Остановимся на этом способе подробнее.
Для графического решения задачи интегрирования произволь - ных функций Лейбниц придумал (1693) механический прибор - интегратор. Если перемещать один штифт этого прибора по графику функции, то другой вычерчивает график первообразной.
Разработанными Лейбницем алгоритмами и обозначениями мы пользуемся и поныне, как и большинством введенных им математических терминов: функция, переменная, постоянная, координаты, абсцисса, алгоритм, дифференциал и др. Многие из этих терминов употреблялись и раньше, но не имели того конкретного значения, которое придал им Лейбниц.
В начале следующего столетия разгорелась бурная дискуссия о приоритете изобретения анализа. Поводом к ней послужила рецензия (1704) Лейбница на работу Ньютона >, где он указал на идейную общность трактовки бесконечно малой у Ньютона и Фабри. Такое сравнение великого англичанина с малоизвестным французским математиком О н о -ре Фабри (1607 - 1688) вызвало > негодование английских ученых. (А Лейбниц не имел никаких задних мыслей; просто книга Фабри была одной из немногих, которая помогла ему в парижский период ликвидировать >.) Они увидели в этом принижение заслуг Ньютона, и началось. В этом споре права Ньютона отстаивали английские ученые, а Лейбница - континентальные. Поддержка Лейбница большинством континентальных математиков объяснялась тем, что его обозначения оказались столь совершенными, а само учение столь доступным, что сразу нашли сторонников среди многих ученых Европы, что бывает крайне редко при появлении новой теории.
По-видимому, именно этот спор имел в виду замечательный русский поэт Валерий Брюсов, когда писал такие строки:
О Лейбниц, о мудрец, создатель вещих книг! Ты выше мира был, как древние пророки. Твой век, дивясь тебе, пророчеств не достиг И с лестью смешивал безумные упреки.
На самом же деле претензии обеих сторон были безоснователь - ными. Оба ученых независимо пришли к созданию дифференциаль - ного и интегрального исчислений, да и подходы у них были совершенно разные. Ньютон использовал аппарат степенных рядов, а Лейбниц - понятие дифференциала. Разгоревшийся спор привел к тому, что английские математики игнорировали все, что исходило от Лейбница и его школы, а континентальные - работы англичан. Поскольку на континенте опирались на более совершен - ную, чем ньютоновская, символику Лейбница и ученые были объединены общими идеями, опубликованными и доступными каждому, то континентальные математики в посленьютоновский период далеко ушли вперед в сравнении с английскими.
Однако в судьбе Лейбница вражда между английскими и континентальными математиками сыграла роковую роль. Герцог, у которого он служил библиотекарем, историком и био - графом, став (1714) английским королем, уехал в Лондон. По - следовать за ним Лейбниц не мог из-за испорченных отношений с английскими математиками. К тому же герцог был недоволен своим историографом, считая, что он недостаточно уделяет вни - мания своим прямым служебным обязанностям. Лейбницу при - шлось остаться и работать в библиотеке герцога. Немилость ново - испеченного английского короля привела к тому, что окружение ученого сильно поредело. Через два года он умер, провожаемый в последний путь только секретарем и могильщиками. Обидная несправедливость судьбы по отношению к великому ученому, которым было сделано очень много.
Несмотря на огромную занятость по составлению истории герцогского дома, превратившейся в историю Западной Европы, и другие отвлекающие от науки обязанности, Лейбниц оставил множество работ по математике, философии, биологии, теории познания, политике, праву, языкознанию. Будучи всесторонне талантливым ученым, он внес неоценимый вклад в каждую из этих областей. Идеи у него сыпались как из рога изобилия: каждое письмо, любая заметка или статья содержали нечто принципиально новое в рассматриваемой области науки, подчас определяющее дальнейшее ее развитие. Многое было сделано при его непосред - ственном участии. В Берлине он организовал научное общество, преобразованное впоследствии в берлинскую АН, и стал первым его президентом. Он был первым иностранным членом Парижской АН. Лейбниц неоднократно встречался в Берлине с Петром I, для которого разработал ряд проектов развития образования и госу - дарственного правления России, а также создания Петербургской АН.
Но наиболее весомым оказался его вклад в математику. Вступив в нее >, он смог полностью ее преобразовать. После его работ и трудов его ближайших сподвижников не только появился математический анализ, но и вся математика вступила в новую эпоху.
